【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论: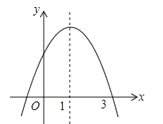
(1)ac>0;
(2)方程ax2+bx+c=0的两根是x1=﹣1,x2=3;
(3)2a﹣b=0;
(4)当x>1时,y随x的增大而减小;
则以上结论中正确的有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:由二次函数y=ax2+bx+c的图象可得:抛物线开口向下,即a<0,
抛物线与y轴的交点在y轴正半轴,即c>0,
ac<0,(1)错误;
由图象可得抛物线与x轴的一个交点为(3,0),又对称轴为直线x=1,
抛物线与x轴的另一个交点为(﹣1,0),
则方程ax2+bx+c=0的两根是x1=﹣1,x2=3,(2)正确.
∵对称轴为直线x=1,
∴﹣![]() =1,即2a+b=0,(3)错误;
=1,即2a+b=0,(3)错误;
由函数图象可得:当x>1时,y随x的增大而减小,故(4)正确;
综上所知正确的有(2)(4)两个,
故选B.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.

-
科目: 来源: 题型:
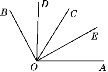
查看答案和解析>>【题目】如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其补角的度数;
(2)①请求出∠DOC和∠AOE的度数;
②判断∠DOE与∠AOB是否互补,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60 cm,求绳子的原长.

-
科目: 来源: 题型:
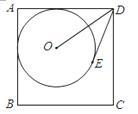
查看答案和解析>>【题目】如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为44,且DE=6,则sin∠ODE=
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形且
 ,求∠B的大小.
,求∠B的大小.
相关试题

