【题目】如图1,将1张菱形纸片ABC的(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD.再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=∠ADB,得到如图2所示的△DB′C,连接AC、BB′,∠DAB=45°,有以下结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= ![]() AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上)
AB,其中正确结论的序号是 . (把所有正确结论的序号都填在横线上) 
参考答案:
【答案】①②③
【解析】解:如图1, 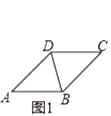
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,∠A=∠C=45°,
∴∠ADB=∠ABD=67.5°,
∴α=2∠ADB=135°,
如图2,
∵将△BCD以D为旋转中心,按逆时针方向旋转角135°,
∴DB=DB′,DC=DA,CB′=AB,∠7=∠3=67.5°,∠6=135°,
在△DBB′中,∠4=∠5= ![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠ABB′=∠3+∠4=90°,∠BB′C=∠5+∠7=90°,
∴AB∥CB′,
而AB=CB′,
∴四边形ABB′C为矩形,
∴AC=BB′,AC⊥AB,所以①②正确,
∵∠CAB=90°,∠1=45°,
∴∠CAD=45°,
而DC=DA,
∴△ADC为等腰直角三角形,
∴∠CDA=90°;BB′= ![]() AB,所以③正确,④错误.
AB,所以③正确,④错误.
所以答案是①②③.
【考点精析】根据题目的已知条件,利用菱形的性质和旋转的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有( )

(1)∠C′EF=32°;(2)∠AEC=148°;(3)∠BGE=64°;(4)∠BFD=116°.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=6,将△ABC沿BC方向平移得到△A′B′C′,连接AA′,若A′B′恰好经过AC的中点O,则AA′的长度为 .
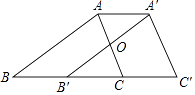
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.

(1)用画树状图或列表法,列出小明、小丽两人一次游戏的所有可能的结果.
(2)求小明获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)

相关试题

