【题目】把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG. 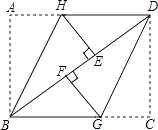
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH= ![]() ∠ABD,∠BDG=
∠ABD,∠BDG= ![]() ∠BDC,
∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG
(2)解:∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD= ![]() =
= ![]() =10,
=10,
∵由(1)知,FD=CD,CG=FG,
∴BF=10﹣6=4cm,
设FG=x,则BG=8﹣x,
在Rt△BGF中,
BG2=BF2+FG2,即(8﹣x)2=42+x2,解得x=3,即FG=3cm
【解析】(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8﹣x,再利用勾股定理即可求出x的值.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
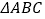 中,
中,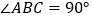 ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作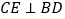 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数
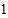 、
、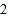 、
、 、
、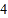 、…、
、…、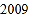 、
、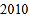 的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________.
的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________. -
科目: 来源: 题型:
查看答案和解析>>【题目】第六次全国人口普查工作圆满结束,2011年5月20日《遵义晚报》报到了遵义市人口普查结果,并根据我市常住人口情况,绘制出不同年龄的扇形统计图;普查结果显示,2010年我市常住人口中,每10万人就有4402人具有大学文化程度,与2000年第五次人口普查相比,是2000年每10万人具有大学文化程度人数的3倍少473人,请根据以上信息,解答下列问题.
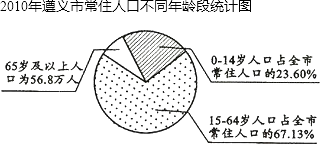
(1)65岁及以上人口占全市常住人口的百分比是;
(2)我市2010年常住人口约为万人(结果保留四个有效数字);
(3)与2000年我市常住人口654.4万人相比,10年间我市常住人口减少万人;
(4)2010年我市每10万人口中具有大学文化程度人数比2000年增加了多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,
 ,
, ,
, ,垂足为E.求证:
,垂足为E.求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线
 的图象与x轴、y轴交于A,B两点,直线
的图象与x轴、y轴交于A,B两点,直线 经过原点,与线段AB交于点C,把
经过原点,与线段AB交于点C,把 的面积分为2:1的两部分,求直线
的面积分为2:1的两部分,求直线 的解析式.
的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划每日生产
 辆自行车,由于人数和操作原因,每日实际生产量分别为
辆自行车,由于人数和操作原因,每日实际生产量分别为 辆、
辆、 辆、
辆、 辆、
辆、 辆、
辆、 辆、
辆、 辆、
辆、 辆.
辆. 用正负数表示每日实际生产量与计划量的增减情况;
用正负数表示每日实际生产量与计划量的增减情况; 该车厂本周实际共生产多少辆自行车?平均每日实际生产多少辆自行车?
该车厂本周实际共生产多少辆自行车?平均每日实际生产多少辆自行车?
相关试题

