【题目】阅读下列材料:
我们知道|x|的几何意义是:在数轴上数x对应的点与原点O的距离,这个结论可以推广为:|x1﹣x2|表示在数轴上数x1,x2对应点之间的距离.
例:解方程|x﹣1|+|x+2|=5.
由绝对值的几何意义知,该方程表示:求在数轴上与1和﹣2的距离之和为5的点对应的数,而在数轴上,1和﹣2的距离为|1﹣(﹣2)|=3,满足方程的x对应点在1的右边或﹣2的左边,若x对应点在1的右边,
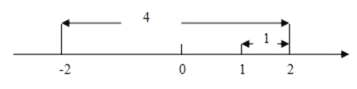
由图可知看出x=2;同理,若x对应点在﹣2的左边,可得x=﹣3,故原方程的解是x=2或x=﹣3.
参考阅读材料,解答下列问题:
(1)方程|x﹣2|+|x+3|=7的解为 .
(2)代数式|x﹣1|+|x+4|的最小值为 .
(3)如图,点A、B、C是数轴上的三点,A点表示数是-3,B点表示数是-1,C点表示数是6,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= .(用含t的代数式表示)
![]()
(4)在(3)的条件下,若mAC﹣4AB的值不随着时间t的变化而改变,试确定m的值.
参考答案:
【答案】(1)x=-4或x=3;(2)5;(3)3t+2, 9+4t;(4)m=3
【解析】
(1)分类讨论:![]() ,根据绝对值的意义,可化简方程,然后解方程,可得答案;
,根据绝对值的意义,可化简方程,然后解方程,可得答案;
(2)代数式|x﹣1|+|x+4|的最小值即为x在1和-4之间时值最小;
(3)根据点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,表示出移动的距离,即可得出AB、AC;
(4)根据mAC﹣4AB的值不随着时间t的变化而改变,可以判断出汗t的项的系数为0,进而能求出m的值.
当![]() 时,原方程可化为
时,原方程可化为
![]() ,解得
,解得![]() ;
;
当![]() 时,原方程等价于
时,原方程等价于![]() ,不存在x的值;
,不存在x的值;
当![]() 时,原方程等价于
时,原方程等价于![]() ,解得
,解得![]() ;
;
故答案为![]() 或
或![]()
代数式|x﹣1|+|x+4|的最小值即为x在1和-4之间时的值
即为![]() ,
,
∴![]()
故答案为![]() .
.
(3)∵A点表示数是-3,B点表示数是-1,C点表示数是6,
∴![]() 原来的距离是:
原来的距离是:![]() ,
,![]() 原来的距离是:
原来的距离是:![]()
∴![]() ,
,![]() ;
;
故填:![]() 、
、![]()
(4)∵mAC﹣4AB=m(4t+9)﹣4(3t+2)=(4m﹣12)t+9m﹣8,
∵mAC﹣4AB的值不随着时间t的变化而改变,
∴4m﹣12=0,
∴m=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
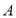 ,
,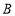 两点在数轴上,点
两点在数轴上,点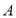 表示的数为-10,点
表示的数为-10,点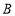 到点
到点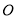 的距离是点
的距离是点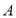 到点
到点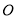 距离的3倍,点
距离的3倍,点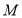 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点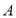 向右运动.点
向右运动.点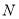 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点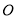 向右运动(点
向右运动(点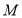 、
、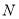 同时出发)
同时出发)
(1)数轴上点
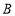 对应的数是______.
对应的数是______.(2)经过几秒,点
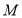 、点
、点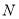 分别到原点
分别到原点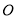 的距离相等.
的距离相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a、b、c 在数轴上的位置如图:
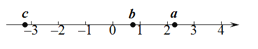
(1)用“<”或“>”填空:a1 0; cb 0; b1 0;
(2)化简:
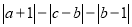 ;
;(3)若abc0,且b与1的距离和c与1的距离相等,求下列式子的值:2b c (a 4c b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最小的正整数,且a、b满足
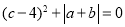 ,请回答问题:
,请回答问题:(1)请直接写出a、b、c的值: a=______; b=________; c=________.
(2)a、b、c所对应的点分别为A、B、C,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,试计算此时BC—AB的值.

(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和x(x>3)个单位长度的速度向右运动,请问:是否存在x,使BC-AB的值随着时间t的变化而不变,若存在求出x;不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
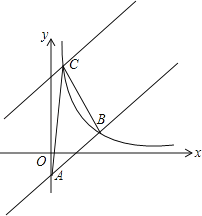
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
相关试题

