【题目】我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
特例探索
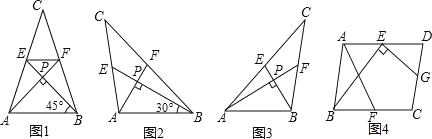
(1)如图1,当∠ABE=45°,c=2![]() 时,a=_____________,b=_____________.
时,a=_____________,b=_____________.
如图2,当∠ABE=30°,c=4时,a=_____________,b=_____________.
归纳证明
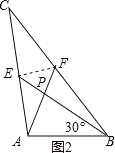
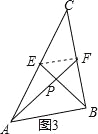
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
拓展应用
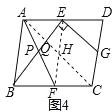
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
参考答案:
【答案】(1)2![]() ,2
,2![]() ,2
,2![]() ,2
,2![]() ;(2)猜想:a2+b2=5c2,证明见解析;(3)4.
;(2)猜想:a2+b2=5c2,证明见解析;(3)4.
【解析】
试题分析:(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=![]() AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=
AB=2,∵AF,BE是△ABC的中线,∴EF∥AB,EF=![]() AB=
AB=![]() ,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=
,∴∠PFE=∠PEF=45°,∴PE=PF=1,在Rt△FPB和Rt△PEA中,AE=BF=![]() =
=![]() ,∴AC=BC=2
,∴AC=BC=2![]() ,∴a=b=2
,∴a=b=2![]() ,如图2,连接EF,同理可得:EF=
,如图2,连接EF,同理可得:EF=![]() ×4=2,∵EF∥AB,∴△PEF~△ABP,∴
×4=2,∵EF∥AB,∴△PEF~△ABP,∴![]() ,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2
,在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=2![]() ,∴PF=1,PE=
,∴PF=1,PE=![]() ,在Rt△APE和Rt△BPF中,AE=
,在Rt△APE和Rt△BPF中,AE=![]() ,BF=
,BF=![]() ,∴a=2
,∴a=2![]() ,b=2
,b=2![]() ,故答案为:2
,故答案为:2![]() ,2
,2![]() ,2
,2![]() ,2
,2![]() ;
;
(2)猜想:a2+b2=5c2,如图3,连接EF,设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得,PF=![]() PA=
PA=![]() ,PE=
,PE=![]() =
=![]() ,AE2=AP2+PE2=c2sin2α+
,AE2=AP2+PE2=c2sin2α+![]() ,BF2=PB2+PF2=
,BF2=PB2+PF2=![]() +c2cos2α,∴
+c2cos2α,∴![]() =c2sin2α+
=c2sin2α+![]() ,
,![]() =
=![]() +c2cos2α,∴
+c2cos2α,∴![]() +
+![]() =
=![]() +c2cos2α+c2sin2α+
+c2cos2α+c2sin2α+![]() ,∴a2+b2=5c2;
,∴a2+b2=5c2;
(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=2![]() ,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=
,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=![]() AD,BF=
AD,BF=![]() BC,∴AE=BF=CF=
BC,∴AE=BF=CF=![]() AD=
AD=![]() ,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,
,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=3,AP=PF,在△AEH和△CFH中,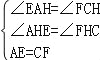 ,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5
,∴△AEH≌△CFH,∴EH=FH,∴EQ,AH分别是△AFE的中线,由(2)的结论得:AF2+EF2=5AE2,∴AF2=5![]() ﹣EF2=16,∴AF=4.
﹣EF2=16,∴AF=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船从甲地顺水开往乙地,所用时间比从乙地逆水开往甲地少1.5小时。已知船在静水中的速度为18千米每小时,水流速度为2千米每小时,求甲乙两地之间的距离?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x 的一次函数,下表列出两套符合条件的课桌椅的高度:
第一套
第二套
椅子高度xcm
40
37
桌子高度ycm
75
70
(1)请确定y与x的函数关系式;
(2)现有一把高39cm的椅子和一张高为72.8的课桌,它们是否配套?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
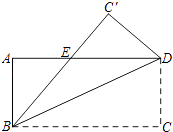
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图2围成一个较大的正方形.
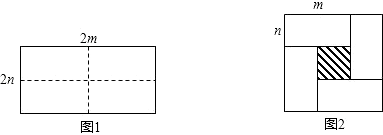
(1)请用两种方法表示图2中阴影部分的面积(只需表示,不必化简);
(2)比较(1)的两种结果,你能得到怎样的等量关系?
(3)请你用(2)中得到的等量关系解决下面问题:如果m﹣n=4,mn=12,求m+n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)

相关试题

