搜索
【题目】某商场购进一种单价为40元的书包，如果以单价50元出售，那么每月可售出30个，根据销售经验，售价每提高5元，销售量相应减少1个．
（1）请写出总的销售利润y元与销售单价提高x元之间的函数关系式；
（2）如果你是经理，为使每月的销售利润最大，那么你确定这种书包的单价为多少元？此时，最大利润是多少元？
参考答案：
【答案】（1）y=（50+x﹣40）（30﹣
）（0≤x≤150）；（2）当这种书包的单价为120元时，每月的销售利润最大为1280元．
【解析】试题分析：（1）根据题意可以求得销售单价提高x元与总的销售利润y元之间的函数关系式；
（2）将（1）中的函数解析式化为顶点式即可解答本题．
试题解析：(1)由题意可得，
即销售单价提高x元与总的销售利润y元之间的函数关系式
(2) 
∴当x=70时，y取得最大值，此时y=1280，
这种书包的单价为：50+70=120．
即为使每月的销售利润最大，这种书包的单价为120元，此时，最大利润是1280元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．
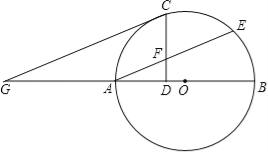
（1）求证：CG是⊙O的切线．
（2）求证：AF=CF．
（3）若∠EAB=30°，CF=2，求GA的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）在数轴上标出数﹣4.5，﹣2，1，3.5所对应的点A，B，C，D；
（2）C，D两点间距离=_____；B，C两点间距离=_____；
（3）数轴上有两点M，N，点M对应的数为a，点N对应的数为b，那么M，N两点之间的距离=_____；
（4）若动点P，Q分别从点B，C同时出发，沿数轴负方向运动；已知点P的速度是每秒1个单位长度，点Q的速度是每秒2个单位长度，问①t为何值时P，Q两点重合？②t为何值时P，Q两点之间的距离为1？
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年9月29日，中国女排以十一连胜的战绩夺得女排世界杯冠军，成为世界三大赛的“十冠王”2019 年女排世界杯的参赛队伍为
支，比赛采取单循环方式，五局三胜，积分规则如下:比赛中以
或者
取胜的球队积
分，负队积
分；而在比赛中以
取胜的球队积
分，负队积
分.前四名队伍积分榜部分信息如下表所示，
(1)中国队
场胜场中只有一场以取胜，请将中国队的总积分填在表格中.(2)巴西队积
分取胜的场次比积分取胜的场次多
场，且负场积分为分，总积分见下表，求巴西队胜场的场数. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点A、点B在数轴上，点C表示－│－3．5│，点D表示－(－2)，点E表示－2
．
（1）点A表示_______，点B表示_______；
（2）在数轴上表示出点C，点D，点E；
（3)比较大小：_______＜_______＜_______＜_______＜_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地，快车比慢车晚出发0.5小时，行驶一段时间后，快车途中休息，休息后继续按原速行驶，到达乙地后停止．慢车和快车离甲地的距离)
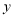(千米)与慢车行驶时间
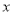(小时)之间的函数关系如图所示．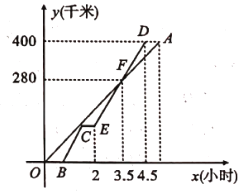
(1)求快车的速度；
(2)求快车到达乙地比慢车到达乙地早了多少小时？
(3)求线段
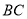对应的函数关系式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，线段AB的端点坐标为A（-2,4），B（4,2），直线y=kx-2与线段AB有交点，则K的值不可能是（ ）
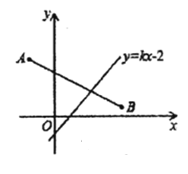
A. -5B. -2C. 3D. 5
相关试题
