Question

【题目】在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB.

(1)若四边形ABCD为正方形．

①如图①，请直接写出AE与DF的数量关系______________；

②将△EBF绕点B逆时针旋转到图②所示的位置，连接AE，DF，猜想AE与DF的数量关系并说明理由；

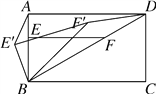
(2)如图③，若四边形ABCD为矩形，BC＝mAB，其他条件都不变，将△EBF绕点B逆时针旋转α(0°＜α＜90°)得到△E′BF′，连接AE′，DF′，请在图③中画出草图，并求出AE′与DF′的数量关系．

Answer 1

【答案】(1)①DF＝ AE

②DF＝AE.理由见解析； (2) DF′＝ AE′.

【解析】试题分析：

（1）①由四边形ABCD是正方形易得BD=AB，由EF∥AD可得，从而可DF=AE；

②由旋转的性质结合题意可证△ABE∽△DBF可得，从而可得DF=AE；

（2）画图如下，由四边形ABCD为矩形，可得AD＝BC＝mAB，由勾股定理可得BD＝＝AB；易证△BEF∽△BAD，可得，因此＝.

由旋转性质结合题意可证△ABE′∽△DBF′，由此可得＝＝，

∴DF′＝ AE′.

试题解析：

(1)①DF＝ AE

②DF＝AE.理由如下：

∵△EBF绕点B逆时针旋转到图②所示的位置，

∴∠ABE＝∠DBF.

∵， ，

∴ ，

∴△ABE∽△DBF，

∴ ，即DF＝ AE.

(2)如图所示，∵四边形ABCD为矩形，

∴AD＝BC＝mAB，

∴BD＝＝AB.

∵EF⊥AB，

∴EF∥AD，

∴△BEF∽△BAD，

∴，

∴＝.

∵△EBF绕点B逆时针旋转α(0°＜α＜90°)得到△E′BF′，

∴∠ABE′＝∠DBF′，BE′＝BE，BF′＝BF，

∴＝＝，

∴△ABE′∽△DBF′，

∴＝＝，即DF′＝ AE′.