【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
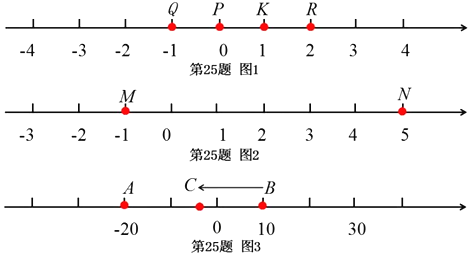
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:
的好点.同理可以判断:
点P__________有序点对![]() 的好点,点R______________有序点对
的好点,点R______________有序点对![]() 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对![]() 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
参考答案:
【答案】(1)不是;是;(2)3;(3)5秒或7.5或10秒或22.5秒或30秒或45秒;
【解析】
可以根据好点的定义判断好点,这种新定义问题通常的解法是照猫画虎.
(1)PQ =![]() PR,RP=2RK
PR,RP=2RK
所以答案为:不是;是
(2) 当点X在点M、N之间,由MN=5-(-1)=6,XM=2XN,
所以XM=4,XN=2,即点X距离点M为4个单位,距离点N为2个单位,
即点X所表示的数为3,
当点X在点N的右边,由MN=5-(-1)=6,XM=2XN,所以XM=12,XN=6,
即点X距离点M为12个单位,距离点N为6个单位,
即点X所表示的数为11;
(3)AB=10-(-20)=30,
当点C在点A、B之间,
若点C为有序点对![]() 的好点,则CA=2CB,CB=10,t=5(秒)
的好点,则CA=2CB,CB=10,t=5(秒)
②若点C为有序点对![]() 的好点,即CB=2CA,CB=20, t=10(秒)
的好点,即CB=2CA,CB=20, t=10(秒)
③若点B为有序点对![]() 的好点或点A为有序点对
的好点或点A为有序点对![]() 的好点,
的好点,
即BA=2BC或AB=2AC,CB=15, t=7.5(秒)
当点A在点C、B之间,
④点A为有序点对![]() 的好点,即AB=2AC,CB=45,t=22.5(秒)
的好点,即AB=2AC,CB=45,t=22.5(秒)
②点C为有序点对![]() 的好点或点B为有序点对
的好点或点B为有序点对![]() 的好点,
的好点,
即CB=2CA或BC=2BA,CB=60,t=30(秒);
③点A为有序点对![]() 的好点,即AC=2AB,CB=90, t=45
的好点,即AC=2AB,CB=90, t=45
∴当经过5秒或7.5或10秒或22.5秒或30秒或45秒时,A、B、C中
恰有一个点为其余两有序点对的好点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=
 ,则CF的长为_______
,则CF的长为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,P为边AB上一点.

(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的妙点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的妙点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的妙点,但点D是(B,A)的妙点.
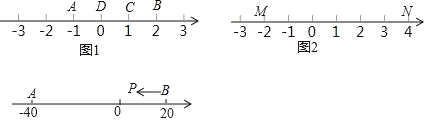
知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的妙点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发向左运动,到达点A停止.P点运动多少个单位时,P、A和B中恰有一个点为其余两点的妙点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2﹣
x2﹣  (b+1)x+
(b+1)x+  (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.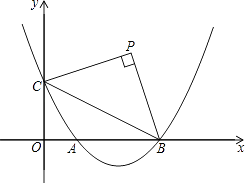
(1)点B的坐标为 , 点C的坐标为(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
相关试题

