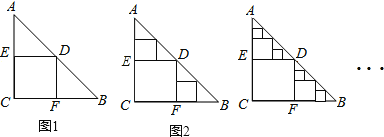
【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是
参考答案:
【答案】![]() ;
;![]() .
.
【解析】
试题分析:根据题意,可求得S△AED+S△DBF=S正方形ECFD=S1=1,同理可得规律:Sn即是第n次剪取后剩余三角形面积和,根据此规律求解即可答案.
试题解析:∵四边形ECFD是正方形,
∴DE=EC=CF=DF,∠AED=∠DFB=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AE=DE=EC=DF=BF=EC=CF,
∵AC=BC=2,
∴DE=DF=1,
∴S△AED+S△DBF=S正方形ECFD=S1=1;
同理:S2即是第二次剪取后剩余三角形面积和,
Sn即是第n次剪取后剩余三角形面积和,
∴第一次剪取后剩余三角形面积和为:2﹣S1=1=S1,
第二次剪取后剩余三角形面积和为:S1﹣S2=1﹣![]() =
=![]() =S2,
=S2,
第三次剪取后剩余三角形面积和为:S2﹣S3=![]() ﹣
﹣![]() =
=![]() =S3,
=S3,
…
第n次剪取后剩余三角形面积和为:Sn﹣1﹣Sn=Sn=![]() .
.
则s10=![]() =
=![]() ;s2012=
;s2012=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,AD平分∠BAC,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是∠EDF的平分线?如果是,请给予证明;如果不是,请说明理由.

(2)若将(1)中的结论与①AD平分∠BAC;②DE∥AB;③DF∥AC这三个条件中的任一个互换,所得命题正确吗?请选择一种情况说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3
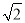 C. 4 D. 4
C. 4 D. 4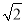
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
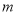 ,
,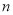 ,
, ,
,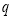 满足
满足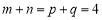 ,
,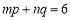 ,则
,则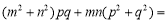 __________.
__________. -
科目: 来源: 题型:
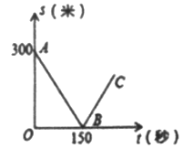
查看答案和解析>>【题目】甲、乙两名自行车爱好者准备在段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系根据图中信息,回答下列问题:
(1)乙的速度为多少米/秒;
(2)当乙追上甲时,求乙距起点多少米;
(3)求线段BC所在直线的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若a,b互为相反数,则
 =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为 分.其中正确的为____(填序号).
分.其中正确的为____(填序号).
相关试题

