【题目】(1)如图,AD平分∠BAC,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是∠EDF的平分线?如果是,请给予证明;如果不是,请说明理由.

(2)若将(1)中的结论与①AD平分∠BAC;②DE∥AB;③DF∥AC这三个条件中的任一个互换,所得命题正确吗?请选择一种情况说明理由.
参考答案:
【答案】(1)是,理由见解析;(2)正确,理由见解析.
【解析】
(1)DE∥AB,DF∥AC得到平行四边形AFDE,因为∠EAD=∠FAD和DE∥AB,推出∠EAD=EDA,得出AE=DE,即可得到答案;
(2)①如和AD是∠CAB的角平分线交换,正确,理由与(1)证明过程相似;②如和DE∥AB交换,根据平行线的性质得到∠FDA=∠EAD,根据AD是∠CAB的角平分线,DO是∠EDF的角平分线,推出∠EAF=∠EDF,由平行线的性质得到∠AEF=∠DFE,根据三角形的内角和定理即可求出∠DEF=∠AFE,根据平行线的判定即可推出答案;③如和AE∥DF交换,正确理由与②类似.
(1)DO是∠EDF的角平分线,证明如下:
∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
∵DE∥AB,
∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴平行四边形AFDE是菱形,
∴DO是∠EDF的角平分线;
(2)正确.
①如和AD平分∠BAC交换,正确,理由如下:
∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,
∵DO是∠EDF的角平分线,
∴∠EDO=∠FDO,
∵DE∥AB,
∴∠DAF=∠EDO,
∴∠DAF=∠FDO,
∴AF=DF,
∴平行四边形AFDE是菱形,
∴AD是∠BAC的角平分线;
②如和DE∥AB交换,正确,理由如下:
∵AD平分∠BAC,
∴∠EAD=∠FAD ,
∵DO是∠EDF的平分线,
∴∠EDA=∠FDA ,
∵DF∥AC,
∴∠EAD=∠FDA ,
∴∠FAD=∠EDA,
∴DE∥AB;
③如和DF∥AC交换,正确,理由如下:
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DO是∠EDF的平分线,
∴∠EDA=∠FDA,
∵DE∥AB,
∴∠EDA=∠FAD,
∴∠EAD=∠FDA,
∴DE∥AB,
综上可知:将(1)中的结论与①AD平分∠BAC;②DE∥AB;③DF∥AC这三个条件中的任一个互换,所得命题正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
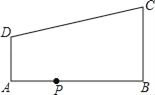
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
-
科目: 来源: 题型:
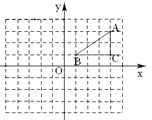
查看答案和解析>>【题目】如图,网格中的每个小正方形的边长均为1个单位长度,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A(4,3),点B(1,1),点C(4,1).
(1)画出Rt△ABC关于y轴对称的Rt△A1B1C1,(点A、B、C的对称点分别是A1、B1、C1),直接写出A1的坐标;
(2)将Rt△ABC向下平移4个单位,得到Rt△A2B2C2(点A、B、C的对应点分别是A2、B2、C2),画出Rt△A2B2C2 ,连接A1C2,直接写出线段A1C2的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3
 C. 4 D. 4
C. 4 D. 4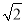
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
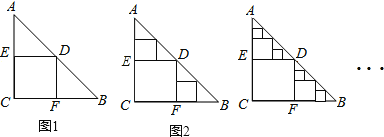
查看答案和解析>>【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是
相关试题

