【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 ![]() 的值为 .
的值为 . 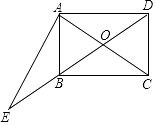
参考答案:
【答案】![]()
【解析】解:作BH⊥OA于H,如图,
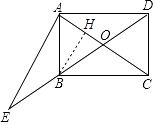
∵四边形ABCD为矩形,
∴OA=OC=OB,∠ABC=90°,
在Rt△ABC中,AC= ![]() =5,
=5,
∴AO=OB= ![]() ,
,
∵ ![]() BHAC=
BHAC= ![]() ABBC,
ABBC,
∴BH= ![]() =
= ![]() ,
,
在Rt△OBH中,OH= ![]() =
= ![]() =
= ![]() ,
,
∵EA⊥CA,
∴BH∥AE,
∴△OBH∽△OEA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】通过灵活运用矩形的性质和相似三角形的判定与性质,掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
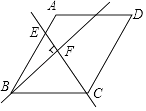
A.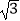
B.2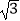
C. π
π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请用两种不同的方法列代数式表示图1中阴影部分的面积.

方法①: ;
方法②: ;
(2)根据(1)写出一个等式: ;
(3)若x+y=8,xy=3.75,利用(2)中的结论,求x,y;
(4)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D做BC边上的高DE,则DE与BC的数量关系是 ,△BCD的面积为 ;
(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由;
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
-
科目: 来源: 题型:
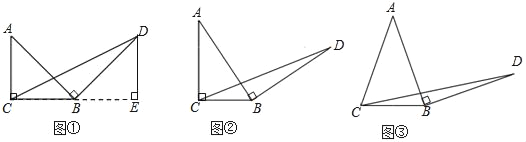
查看答案和解析>>【题目】阅读并完成下列证明:如图,AB∥CD,∠B=55°,∠D=125°,求证:BC∥DE.
证明:AB∥CD(已知),
∴∠C=∠B( ),又∵∠B=55°( ),
∴∠C=______°(等量代换),
∵∠D=125°( ),
∴
∴BC∥DE( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(
 ,
, m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )A. x>
 B.
B.  <x<
<x< C. x<
C. x< D. 0<x<
D. 0<x<
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别
阅读时间t(单位:小时)
频数(人数)
A
0≤t<1
8
B
1≤t<2
20
C
2≤t<3
24
D
3≤t<4
m
E
4≤t<5
8
F
t≥5
4
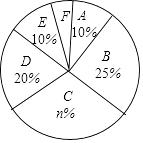
(1)图表中的m= , n=;
(2)扇形统计图中F组所对应的圆心角为度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?
相关试题

