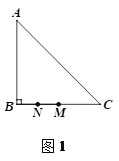
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
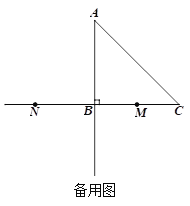
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)①根据题意补充图形即可;
②连接AD.在Rt△ABN中,由勾股定理得AN的长.由平移的性质得到DM=AN,
进而得到△ADP∽△CMP,由相似三角形的性质即可得到结论.
(2)连接![]() ,先证四边形
,先证四边形![]() 是平行四边形.由平行四边形的性质得到
是平行四边形.由平行四边形的性质得到![]() ∥
∥![]() ,再由平行线的性质得到
,再由平行线的性质得到![]() .进而得到
.进而得到![]() .由平行线分线段成比例定理得到
.由平行线分线段成比例定理得到![]() .由此得到NB的长,即可得到结论.
.由此得到NB的长,即可得到结论.
详解:(1)①如图1,补全图形.
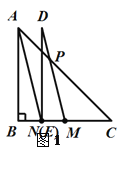
② 连接AD,如图2.
在Rt△ABN中,∵∠B=90°,AB=4,BN=1,∴![]() .
.
∵线段AN平移得到线段DM,∴DM=AN=![]() ,AD=NM=1,AD∥MC,
,AD=NM=1,AD∥MC,
∴△ADP∽△CMP.
∴![]() .
.
∴![]() .
.

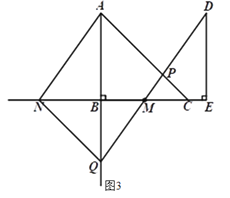
(2)连接![]() ,如图3.
,如图3.
由平移知:![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ∥
∥![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
又∵![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
∴![]() .
.
∴![]() (舍去负数).
(舍去负数).
∴![]() .
.
∴![]() .
.
方法二,连接AD,如图4.

设CE长为x.
∵线段AB移动到得到线段DE,
∴![]() ,AD∥BM.
,AD∥BM.
∴△ADP∽△CMP.
∴![]() .
.
∵MQ=DP,
∴![]() .
.
∵△QBM∽△QAD,
∴![]() .
.
解得:![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,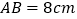 ,点
,点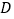 是
是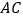 边的中点,点
边的中点,点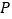 是边
是边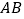 上的一个动点,过点
上的一个动点,过点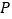 作射线
作射线 的垂线,垂足为点
的垂线,垂足为点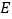 ,连接
,连接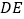 .设
.设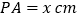 ,
,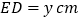 .
.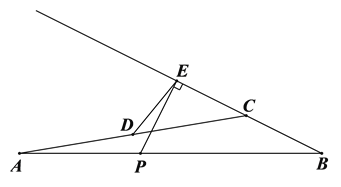
小石根据学习函数的经验,对函数
 随自变量
随自变量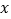 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了
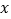 与
与 的几组值,如下表:
的几组值,如下表: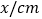
0
1
2
3
4
5
6
7
8
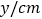
3.0
2.4
1.9
1.8
2.1
3.4
4.2
5.0
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
点
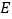 是
是 边的中点时,
边的中点时,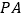 的长度约为
的长度约为 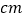 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
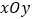 中,抛物线
中,抛物线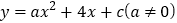 经过点
经过点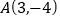 和
和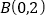 .
.(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线
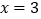 翻折,得到图象N.若过点
翻折,得到图象N.若过点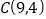 的直线
的直线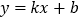 与图象M、图象N都相交,且只有两个交点,求b的取值范围.
与图象M、图象N都相交,且只有两个交点,求b的取值范围. -
科目: 来源: 题型:
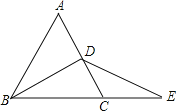
查看答案和解析>>【题目】已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
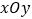 中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.(1)已知,点
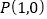 ,
,①点
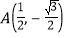 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);②点
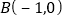 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);(2)若点P在
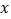 轴上,且点P的“伴随圆”与直线
轴上,且点P的“伴随圆”与直线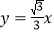 相切,求点P的坐标;
相切,求点P的坐标; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视机厂要印制产品宜传材料甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙厂提出:每份材料收2.5元印制费,不收制版费.
(1)分别写出两厂的收费
 元与印制数量
元与印制数量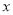 (份)之间的关系式
(份)之间的关系式(2)在同一直角坐标系内画出它们的图象;
(3)根据图像回答下列问题:
①印制800份宣传材料时,选择哪家印刷厂比较合算?
②电视机厂拟拿出3000元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
相关试题

