【题目】在平面直角坐标系![]() 中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
(1)已知,点![]() ,
,
①点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
②点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
(2)若点P在![]() 轴上,且点P的“伴随圆”与直线
轴上,且点P的“伴随圆”与直线![]() 相切,求点P的坐标;
相切,求点P的坐标;
参考答案:
【答案】(1)上;外;(2)点P (2,0)或(2,0).
【解析】分析:(1)计算PA、PB的长,然后与半径1比较大小即可得出结论;
(2)连接PH,由点![]() 的“伴随圆”与直线
的“伴随圆”与直线![]() 相切,得到PH⊥OH,PH=1,∠POH=30°,则OP=2,由此即可得到结论.
相切,得到PH⊥OH,PH=1,∠POH=30°,则OP=2,由此即可得到结论.
详解:(1)①PA=![]() =1.
=1.
故选A在⊙P上.故答案为:上;
②PB=![]() =2>半径1,∴B在⊙P外.故答案为:外.
=2>半径1,∴B在⊙P外.故答案为:外.
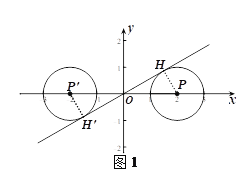
(2)连接![]() ,如图1.
,如图1.
∵点![]() 的“伴随圆”与直线
的“伴随圆”与直线![]() 相切,
相切,
∴PH⊥OH,
∴PH=1,∠POH=30°,
可得:OP=2,
∴点P(2,0)或(-2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
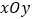 中,抛物线
中,抛物线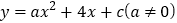 经过点
经过点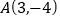 和
和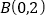 .
.(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线
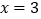 翻折,得到图象N.若过点
翻折,得到图象N.若过点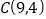 的直线
的直线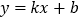 与图象M、图象N都相交,且只有两个交点,求b的取值范围.
与图象M、图象N都相交,且只有两个交点,求b的取值范围. -
科目: 来源: 题型:
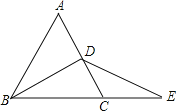
查看答案和解析>>【题目】已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,求DE的长.
-
科目: 来源: 题型:
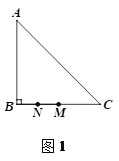
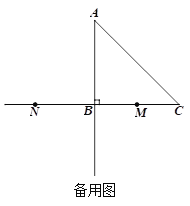
查看答案和解析>>【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视机厂要印制产品宜传材料甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙厂提出:每份材料收2.5元印制费,不收制版费.
(1)分别写出两厂的收费
 元与印制数量
元与印制数量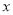 (份)之间的关系式
(份)之间的关系式(2)在同一直角坐标系内画出它们的图象;
(3)根据图像回答下列问题:
①印制800份宣传材料时,选择哪家印刷厂比较合算?
②电视机厂拟拿出3000元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,E为BC边上一点,且AE交DC延长线于F,连接BF,下列关于面积的结论中错误的是( )
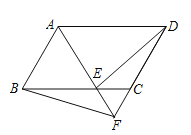
A.S△ABF =S△ADEB.S△ABF =S△ADF
C.S△ABF=
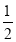 S□ABCDD.S△ADE=
S□ABCDD.S△ADE=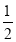 S□ABCD
S□ABCD
相关试题

