【题目】某电子科技公司开发一种新产品,公司对经营的盈亏情况每月最后一天结算1次.在1~12月份中,公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系式y=a(x﹣h)2+k,二次函数y=a(x﹣h)2+k的一部分图象如图所示,点A为抛物线的顶点,且点A、B、C的横坐标分别为4、10、12,点A、B的纵坐标分别为﹣16、20.
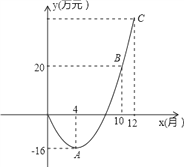
(1)试确定函数关系式y=a(x﹣h)2+k;
(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
参考答案:
【答案】(1)y=x![]() -8x; (2)前9个月9万元。 10月份获利润11万元(3)12月利润最大 最大15万元.
-8x; (2)前9个月9万元。 10月份获利润11万元(3)12月利润最大 最大15万元.
【解析】试题分析:(1)根据题意此抛物线的顶点坐标为(4,-16),设出抛物线的顶点式,把(10,20)代入即可求出a的值,把a的值代入抛物线的顶点式中即可确定出抛物线的解析式;
(2)令(1)求出的抛物线的解析式中的x=9,即可求出前9个月公司累积获得的利润,然后令x=10求出前10个月公司累积获得的利润,两者相减即可求出10月份一个月内所获得的利润;
(3)根据前n个月内所获得的利润减去前n-1个月内所获得的利润,再减去16即可表示出第n个月内所获得的利润,为关于n的一次函数,且为增函数,得到n取最大为12时,把n=12代入即可求出最多的利润.
试题解析:(1)根据题意可设:y=a(x4) 16,
当x=10时,y=20,所以a(104) 16=20,
解得a=1,
所求函数关系式为:y=(x4) 16=x-8x;
(2)当x=9时,y=(94) 16=9,
所以前9个月公司累积获得的利润为9万元,
又由题意可知,当x=10时,y=20,而209=11,
所以10月份一个月内所获得的利润11万元;
(3)设在前12个月中,第n个月该公司一个月内所获得的利润为s(万元),
则有:s=(n4) 16[(n14) 16]=2n9,
因为s是关于n的一次函数,且2>0,s随着n的增大而增大,
而n的最大值为12,所以当n=12时,s=15,
所以第12月份该公司一个月内所获得的利润最多,最多利润是15万元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】要调查你校学生学业负担是否过重,选用下列哪种方法最恰当( )
A.查阅文献资料
B.对学生问卷调查
C.上网查询
D.对校领导问卷调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
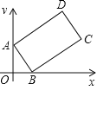
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
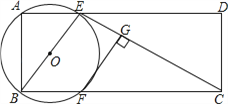
(1)当点F是BC的中点时,求证:直线FG与⊙O相切;
(2)若FG∥BE时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】收集数据常用的方法有 、 、查阅资料等.调查又分为 调查、 调查和抽样调查等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A.购买一张彩票,中奖B.射击运动员射击一次,命中靶心
C.任意画一个三角形,其内角和是180°D.经过有交通信号灯的路口,遇到红灯
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,
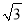 ≈1.73)
≈1.73)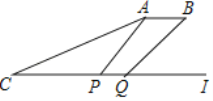
相关试题

