【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.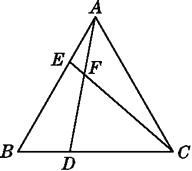
(1)求证:AD=CE;
(2)求∠DFC的度数.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE 。
(2)解:∵ △AEC≌△BDA,
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°
【解析】(1)根据等边三角形的性质得出∠BAC=∠B=60°,AB=AC ,然后利用SAS判断出△AEC≌△BDA ,根据全等三角形对应边相等得出AD=CE ;
(2)根据全等三角形对应角相等得出∠ACE=∠BAD,根据三角形的外角定理及等量代换得出∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60° 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长线上,且CE=1,∠E=30°,则BC=
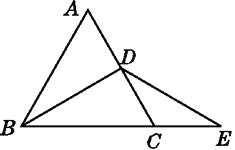
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是随机事件的是( )
A.购买一张福利彩票,中特等奖
B.在一个标准大气压下,加热水到100℃,沸腾
C.任意三角形的内角和为180°
D.在一个仅装着白球和黑球的袋中摸出红球 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,F是BE,CD的交点.请写出图中两对全等的三角形,并选出其中一对加以证明.
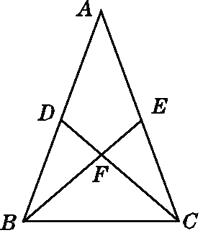
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD中,AD∥BC,连接AC,E、F分别为AC、CB的中点,BC=2AD,
 ,
,则四边形ABCD的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况
下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
技术
上场时间
(分钟)
出手投篮(次)
投中
(次)
罚球
得分
篮板
(个)
助攻
(次)
个人
总得分
数据
45
27
14
7
13
12
41
【注:表中出手投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚
球得分.】根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证:
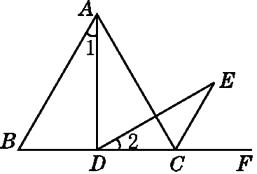
(1)∠1=∠2;
(2)AD=DE.
相关试题

