【题目】如图(1)我们知道等腰直角三角形的三边的比AC:BC:AB=1:1: ![]() ,含有30度的直角三角形的三边之比AC:BC:AB=1∶
,含有30度的直角三角形的三边之比AC:BC:AB=1∶![]() ∶2.如图(2),分别取反比例函数
∶2.如图(2),分别取反比例函数![]() ,
, ![]() 图象的一支,Rt△AOB中,OA⊥OB,OA=OB=2,AB交y轴于C,∠AOC=60°,点A,点B分别在这两个图像上。
图象的一支,Rt△AOB中,OA⊥OB,OA=OB=2,AB交y轴于C,∠AOC=60°,点A,点B分别在这两个图像上。
(1)填空: K1=-__________,K2=______________.
(2)将△AOC沿y轴折叠得△DOC,如图所示。
①试判断D点是否存在![]() 的图象上,并说明理由.
的图象上,并说明理由.
②在y轴上找一点N,使得|BN-DN|的值最大,求出点N的坐标。
③连接BD,求S四边形OCBD.
(3)将Rt△AOB绕着原点顺时针旋转一周,速度是5°/秒。问:经过多少秒,直线AB与图中![]() 分支的对称轴或者与图中
分支的对称轴或者与图中![]() 分支的对称轴平行。直接写出结果。
分支的对称轴平行。直接写出结果。

参考答案:
【答案】(1)K1=![]() ,K2=
,K2=![]() (2)①算出D(
(2)①算出D(![]() ),在图像上②N(0,
),在图像上②N(0, ![]() )③
)③![]() (3)12,48,30,66
(3)12,48,30,66
【解析】试题分析:
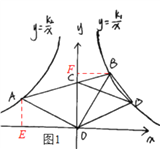
(1)如图1,过点A作AE⊥y轴于点E,过点B作BF⊥y轴于点F,由已知条件即可求得AE、OD、BF和OF的长,结合点A和点B所处象限即可得到点A、B的坐标,这样即可求得k1和k2的值了;
(2)①由点A的坐标可得点D的坐标,将点D的坐标代入![]() 中检验即可得出结论;
中检验即可得出结论;
②如图2,延长DB交y轴于点N,此时|BN-DN|的值最大,由B、D的坐标用待定系数法求出直线BD的解析式,再由解析式即可求得直线BD与y轴的交点N的坐标了;
③由AB的坐标求出直线AB的解析式,由此求出点C的坐标,再过点B作y轴的垂线,过点D作x轴的垂线,利用两垂线与两坐标轴围成一个矩形结合已知条件即可求出四边形OCBD的面积了;
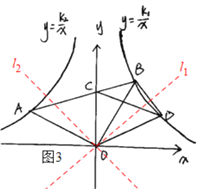
(3)如图3,两个反比例函数图象的分支的对称轴分别是直线l1和l2,它们与x轴相交形成的锐角度数都是45°,由图可知,当△AOB绕点O顺时针旋转60°和240°时,AB与l2平行,当旋转150°和330°时,AB和l1平行,由此结合旋转速度为5°/秒即可求得对应的时间了.
试题解析:
(1)如图1,过点A作AE⊥y轴于点E,过点B作BF⊥y轴于点F,
∴∠AEO=∠BFO=90°,
∵∠AOC=60°,
∴∠AOE=30°,∠BOF=30°,
∴AE:OE:OA=BF:OF:OB=1∶![]() ∶2,
∶2,
又∵∵OA=OB=2,
∴AE=BF=1,OE=OF=![]() ,
,
∴点A、B的坐标分别为![]() 和
和![]() ,
,
∴![]() ,
, ![]() ;
;
(2)①∵点D和点A![]() 关于y轴对称,
关于y轴对称,
∴点D的坐标为![]() ,
,
∴![]() ,
,
∴点D在![]() 的图象上;
的图象上;
②延长DB交y轴于点N,此时|BN-DN|的值最大,
设直线BD的解析式为![]() ,则由B、D的坐标可得:
,则由B、D的坐标可得: 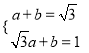 ,
,
解得: 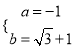 ,
,
∴BD的解析式为: ![]() ,
,
∴点N的坐标为![]() ;
;
③设直线AB的解析式为![]() ,
,
∵点A、B的坐标分别为![]() 和
和![]() ,
,
∴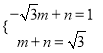 ,解得
,解得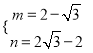 ,
,
∵直线AB与y轴相交于点C,
∴点C的坐标为![]() ,
,
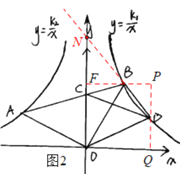
如图2,过点B作BF⊥y轴于点F,过点D作DQ⊥x轴于点Q,FB与DQ相交于点P,
∵点B、D的坐标分别为![]() ,
, ![]() ,
,
∴S四边形OCBD=S矩形OFPQ-S△CFB-S△BDP-S△ODQ
=![]()
=![]()
=![]() ;
;
(3)如图3,由题意可知,两个反比例函数图象的分支的对称轴分别是直线l1和l2,它们与x轴相交形成的锐角度数都是45°,
由图结合∠AOC=60°可知,当△AOB绕点O顺时针旋转60°和240°时,AB与l2平行,当旋转150°和330°时,AB和l1平行,
又∵△AOB绕点O旋转的速度为5°/秒,
∴60÷5=12(秒),150÷5=30(秒),240÷5=48(秒),330÷5=66(秒),
∴当△AOB绕点O旋转12秒、30秒、48秒和66秒时,AB和两个反比例函数图象的一个分支的对称轴平行.
-
科目: 来源: 题型:
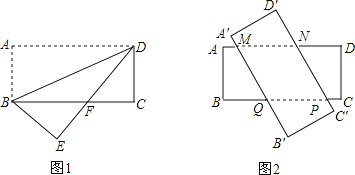
查看答案和解析>>【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某商铺经营某种旅游纪念品.该商铺第一次批发购进该纪念品共花费3 000元,很快全部售完.接着,该商铺第二次批发购进该纪念品共花费9000元.已知第二次所购进该纪念品的数量是第一次的2倍还多300个,第二次的进价比第一次的进价提高了20%.
(1)求第一次购进该纪念品的进价是多少元?
(2)若该纪念品的两次售价均为9元/个,两次所购纪念品全部售完后,求该商铺两次共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=
 ∠BAE;
∠BAE;(2)求证:PG=PB;
(3)若AB=
 ,BC=3,求出BG的长.
,BC=3,求出BG的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE与AC的延长线相交于点E.
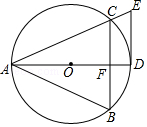
(1)求证:DE∥BC;
(2)若DF=n,∠BAC=2a,写出求CE长的思路.
相关试题

