【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
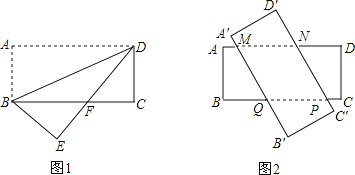
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
参考答案:
【答案】①BF=![]() ②
②![]()
【解析】试题分析:
(1)由折叠的性质结合AD∥BC易得∠FBD=∠ADB=∠FDB,由此可得BF=DF,设BF=x,结合DE=AD=BC=8,可得EF=8-x,结合BE=AB=3,在Rt△BEF中由勾股定理建立方程即可求得BF的值;
(2)①如图3,过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,则易证△QEP≌△NFP,从而可得PQ=PN,由已知条件易证四边形MNPQ是平行四边形,两者结合即可得到四边形MNPQ是菱形;
②如图4,由题意可知,菱形MNPQ边上的高是3,故当边长越长时,面积越大,由题意可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,在Rt△ABQ中,由勾股定理建立方程解出MQ的长,即可求得最大面积了.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=8,
∴∠ADB=∠DBC,
由折叠的性质可知,∠ADB=∠FDB,BE=AB=3,DE=AD=8,
∴∠DBC=∠FDB,
∴BF=DF,
设BF=x,则DF=x,
∴EF=8-x,
∵在Rt△BEF中,BF2=BE2+EF2,
∴![]() ,解得:
,解得: ![]() ;
;
(2)①如图2,四边形MNPQ是菱形,理由如下:
过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,
∴∠PEQ=∠PFN=90°,
∵两张纸条等宽,
∴NF=QE,
∵∠NPF=∠QPE,
∴△QEP≌△NFP,
∴PQ=PN,
∵由题意可得:MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形,
∴四边形MNPQ是菱形;

②如图4,由题意和①可知,菱形MNPQ边上的高是3,故当菱形MNPQ的边长越长时,其面积越大,由图4可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,
设AQ=QP=a,则BQ=BC-QC=8-a,
∵在Rt△ABQ中,AQ2=AB2+BQ2,
∴![]() ,解得:
,解得: ![]() ,
,
∴菱形MNPQ的最大面积为: ![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试
面 试
体 能
甲
85
80
75
乙
80
90
73
丙
83
79
90
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.
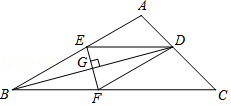
(1)求证:DE=DF;
(2)若∠ABC=30°,∠C=45°,DE=4,求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料: 2017年1月28日至2月1日农历正月初一至初五,平谷区政府在占地面积6万平方米的琴湖公园举办主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会.
本次庙会共设置了文艺展演区、非遗展示互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区.展区总面积1720平方米.文艺展演区占地面积600平方米,占展区总面积的34.9%;非遗展示区占地190平方米,占展区总面积的11.0%;特色商品区占地面积是文艺展演区的一半,占展区总面积的17.4%;特色美食区占地200平方米,占展区总面积的11.6%;还有孩子们喜爱的儿童娱乐游艺区.
此次庙会本着弘扬、挖掘、展示平谷春节及民俗文化,以京津冀不同地域的特色文化为出发点,全面展示平谷风土人情及津冀人文特色.大年初一,来自全国各地的约3.2万人踏着新春的脚步,揭开了首届平谷庙会的帷幕.大年初二尽管天气寒冷,市民逛庙会热情不减,又约有4.3万人次参观了庙会,品尝特色美食,观看绿都古韵、秧歌表演、天桥绝活,一路猜灯谜、赏图片展,场面火爆.琳琅满目的泥塑、木版画、剪纸、年画等民俗作品也让游客爱不释手,纷纷购买.大年初三,单日接待游客约4万人次,大年初四风和日丽的天气让庙会进入游园高峰,单日接待量较前日增长了约50%.大年初五,活动进入尾声,但庙会现场仍然人头攒动,仍约有5.5万人次来园参观.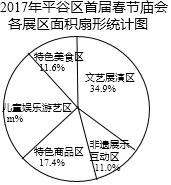
(1)直接写出扇形统计图中m的值;
(2)初四这天,庙会接待游客量约万人次;
(3)请用统计图或统计表,将庙会期间每日接待游客的人数表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某商铺经营某种旅游纪念品.该商铺第一次批发购进该纪念品共花费3 000元,很快全部售完.接着,该商铺第二次批发购进该纪念品共花费9000元.已知第二次所购进该纪念品的数量是第一次的2倍还多300个,第二次的进价比第一次的进价提高了20%.
(1)求第一次购进该纪念品的进价是多少元?
(2)若该纪念品的两次售价均为9元/个,两次所购纪念品全部售完后,求该商铺两次共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=
 ∠BAE;
∠BAE;(2)求证:PG=PB;
(3)若AB=
 ,BC=3,求出BG的长.
,BC=3,求出BG的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)我们知道等腰直角三角形的三边的比AC:BC:AB=1:1:
 ,含有30度的直角三角形的三边之比AC:BC:AB=1∶
,含有30度的直角三角形的三边之比AC:BC:AB=1∶ ∶2.如图(2),分别取反比例函数
∶2.如图(2),分别取反比例函数 ,
,  图象的一支,Rt△AOB中,OA⊥OB,OA=OB=2,AB交y轴于C,∠AOC=60°,点A,点B分别在这两个图像上。
图象的一支,Rt△AOB中,OA⊥OB,OA=OB=2,AB交y轴于C,∠AOC=60°,点A,点B分别在这两个图像上。(1)填空: K1=-__________,K2=______________.
(2)将△AOC沿y轴折叠得△DOC,如图所示。
①试判断D点是否存在
 的图象上,并说明理由.
的图象上,并说明理由. ②在y轴上找一点N,使得|BN-DN|的值最大,求出点N的坐标。
③连接BD,求S四边形OCBD.
(3)将Rt△AOB绕着原点顺时针旋转一周,速度是5°/秒。问:经过多少秒,直线AB与图中
 分支的对称轴或者与图中
分支的对称轴或者与图中 分支的对称轴平行。直接写出结果。
分支的对称轴平行。直接写出结果。
相关试题

