【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
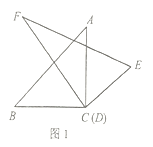
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
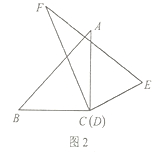
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
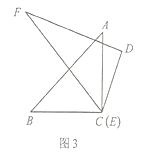
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() , 理由见解析;(3)
, 理由见解析;(3)![]() .
.
【解析】
(1)利用角平分线的定义求出∠ACF=45°,然后利用余角的性质求解即可;
(2)依据同角的余角相等即可求解;
(3)∠ACD与∠BCF都与∠ACF关系紧密,分别表示它们与∠ACF的关系即可求解.
(1)∵CF是∠ACB的平分线,∠ACB=90°,
∴∠ACF=90°÷2=45°,
又∵∠FCE=90°,
∴∠ACE=∠FCE﹣∠ACF=90°﹣45°=45°;
(2)∵∠BCF+∠ACF=90°,
∠ACE+∠ACF=90°,
∴∠BCF=∠ACE;
(3)∵∠FCA=∠FCD﹣∠ACD=60°﹣∠ACD,
∠FCA=∠ACB﹣∠BCF=90°﹣∠BCF,
∴60°﹣∠ACD=90°﹣∠BCF,
∠ACD=30°﹣∠BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多20元,而用800元购买A种零件的数量和用600元购买B种零件的数量相等
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

-
科目: 来源: 题型:
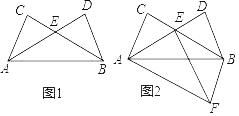
查看答案和解析>>【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(新定义):A、B、C 为数轴上三点,若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍,我们就称点
C 是(A,B)的幸运点.
(特例感知):
(1)如图 1,点 A 表示的数为﹣1,点 B 表示的数为 3.表示 2 的点 C 到点 A 的距离是 3, 到点 B 的距离是 1,那么点 C 是(A,B)的幸运点.
①(B,A)的幸运点表示的数是 ;A.﹣1; B.0; C.1; D.2
②试说明 A 是(C,E)的幸运点.
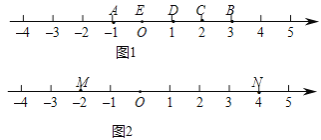
(2)如图 2,M、N 为数轴上两点,点 M 所表示的数为﹣2,点 N 所表示的数为 4,则(M,N)的幸点示的数为 .
(拓展应用):
(3)如图 3,A、B 为数轴上两点,点 A 所表示的数为﹣20,点 B 所表示的数为 40.现有一只电子蚂蚁 P 从点 B 出发,以 3 个单位每秒的速度向左运动,到达点 A 停止.当 t 为何值时,P、A 和 B 三个点中恰好有一个点为其余两点的幸运点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
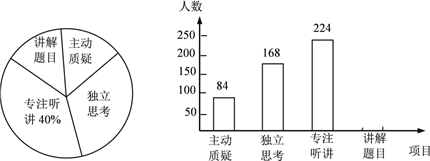
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )

A. y=x+12 B. y=0.5x+12
C. y=0.5x+10 D. y=x+10.5
相关试题

