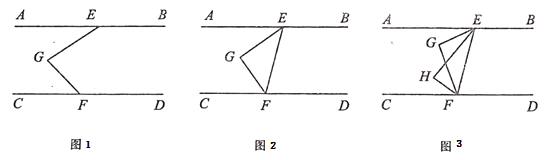
【题目】(1)如图1,已知AB∥CD,求证:∠EGF=∠AEG+∠CFG
(2)如图2,已知AB∥CD,∠AEF与∠CFE的平分线交于点G.猜想∠G的度数。证明你的猜想
(3)如图3,已知AB∥CD,EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,∠G=95°,求∠H的度数.
参考答案:
【答案】(1)见解析;(2)∠G=90°;证明见解析;(3)∠H=85°.
【解析】
(1)过点G作GH∥AB,根据两直线平行内错角相等可证得结论;
(2)由(1)得∠EGF=∠AEG+∠CFG,根据EG、FG分别平分∠AEF和∠CFE,得到∠AEF=2∠AEG,∠CFE=2∠CFG,由于AB∥CD得到∠AEF+∠CFE=180°,于是得到2∠AEG+2∠CFG=180°,即可得到结论;
(3)由(1)得∠G=∠AEG+∠CFG,∠H=∠AEH+∠CFH,根据EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,分别得到∠AEG=∠GEH=∠HEF=![]() ∠AEF,∠CFH=∠HFG=∠EFG=
∠AEF,∠CFH=∠HFG=∠EFG=![]() ∠CFE,结合∠AEF+∠CFE=180°,于是可求出∠CFE=105°,∠AEF=75°,代入∠H=
∠CFE,结合∠AEF+∠CFE=180°,于是可求出∠CFE=105°,∠AEF=75°,代入∠H=![]() ∠AEF+
∠AEF+![]() ∠CFE,计算即可得到结论.
∠CFE,计算即可得到结论.
解:(1)如图1,
过点G作GH∥AB,
∴∠EGH=∠AEG.
∵AB∥CD,
∴GH∥CD.
∴∠FGH=∠CFG.
∴∠EGH+∠FGH=∠AEG+∠CFG.
即∠EGF=∠AEG+∠CFG;
(2)猜想:∠G=90°;
证明:如图2,
由(1)中的结论得:∠EGF=∠AEG+∠CFG,
∵EG、FG分别平分∠AEF和∠CFE,
∴∠AEF=2∠AEG,∠CFE=2∠CFG,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2∠AEG+2∠CFG=180°,
∴∠AEG+∠CFG=90°,
∴∠G=90°;
(3)解:如图3,
∵EG平分∠AEH,EH平分∠GEF,FH平分∠CFG,FG平分∠HFE,
∴∠AEG=∠GEH=∠HEF=![]() ∠AEF,∠CFH=∠HFG=∠EFG=
∠AEF,∠CFH=∠HFG=∠EFG=![]() ∠CFE,
∠CFE,
由(1)可知,∠G=∠AEG+∠CFG,∠H=∠AEH+∠CFH,
∴∠G=![]() ∠AEF+
∠AEF+![]() ∠CFE=95°,
∠CFE=95°,
∴![]() (∠AEF+∠CFE)+
(∠AEF+∠CFE)+![]() ∠CFE=95°,
∠CFE=95°,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠CFE=105°,
∴∠AEF=75°,
∴∠H=![]() ∠AEF+
∠AEF+![]() ∠CFE=
∠CFE=![]() ×75°+
×75°+![]() ×105°=85°.
×105°=85°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将
 沿
沿 翻折,点
翻折,点 的对称点是点
的对称点是点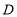 ,
, ,
,(1)求证:四边形
 是菱形;
是菱形;(2)如图2,在
 上取一点
上取一点 ,连接
,连接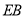 并延长至点
并延长至点 ,在
,在 上取一点
上取一点 ,连接
,连接 ,若
,若 ,求证:
,求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直角三角形的直角顶点放在点
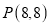 处,两直角边与坐标轴交于如图所示的点
处,两直角边与坐标轴交于如图所示的点 和点
和点 ,则
,则 的值为______.
的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?

相关试题

