Question

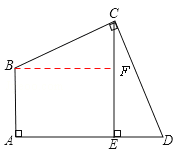
【题目】如图，四边形ABCD中，∠A=∠BCD=90°，BC=CD，CE⊥AD，垂足为E，求证：AE=CE．

Answer 1

【答案】证明：如图，过点B作BF⊥CE于F，

∵CE⊥AD，∴∠D+∠DCE=90°。

∵∠BCD=90°，∴∠BCF+∠DCE=90°。

∴∠BCF=∠D。

在△BCF和△CDE中，∵，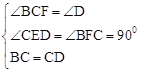

∴△BCF≌△CDE（AAS）。∴BF=CE。

又∵∠A=90°，CE⊥AD，BF⊥CE，∴四边形AEFB是矩形。∴AE=BF。

∴AE=CE。

【解析】过点B作BF⊥CE于F，根据同角的余角相等求出∠BCF＝∠D，再利用“角角边”证明△BCF和△CDE全等，根据全等三角形对应边相等可得BF＝CE，再证明四边形AEFB是矩形，根据矩形的对边相等可得AE＝BF，从而得证．