【题目】小明每天上午9时骑自行车离开家,15时回家,他描绘了离家的距与时间的变化情况.
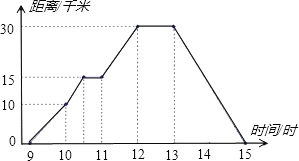
(1)图象表示哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方时什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他由离家最远的地方返回的平均速度是多少.
参考答案:
【答案】(1)图象表示了距离与时间,时间是自变量,距离是因变量.
(2)10时,他离家15千米,13时,他离家30千米;
(3)他到达离家最远的地方是12时,离家30千米;
(4)由图象可以看出从11时到12时他行驶了15千米;
(5)共用了2时,因此平均速度为30÷2=15千米/时.
【解析】解:(1)图象表示了距离与时间,时间是自变量,距离是因变量.
(2)10时,他离家15千米,13时,他离家30千米;
(3)他到达离家最远的地方是12时,离家30千米;
(4)由图象可以看出从11时到12时他行驶了15千米;
(5)共用了2时,因此平均速度为30÷2=15千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=
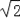 ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市居民用水实行阶梯收费每户每月用水量如果未超过20t,按每吨2.5元收费.如果超过20t,未超过的部分按每吨2.5元收费,超过的部分按每吨3.3元收费.设某户每月用水量为xt,应收水费为y元.
(1)分别写出每月用水量未超过20t和超过20t时y与x间的关系式.
(2)若该城市某户4月份水费平均为每吨2.8元,求该户4月份用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表所示.
所挂物体的质量
0
1
2
3
4
5
6
7
弹簧的长度
12
12.5
13
13.5
14
14.5
15
15.5
(1)上表反映了哪些变量之间的关系?哪个是自变量,哪个是因变量?
(2)当物体的质量为2kg时,弹簧的长度是多少?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25
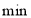 ,于是立即步行回家取票同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父子俩送票、取票过程中离体育馆的路程
,于是立即步行回家取票同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父子俩送票、取票过程中离体育馆的路程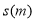 与所用时间
与所用时间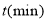 之间的图像,结合图像解答下列问题(假设骑自行车和步行的速度始终保持不变):
之间的图像,结合图像解答下列问题(假设骑自行车和步行的速度始终保持不变):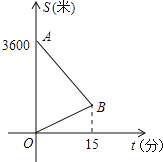
(1)图中O点表示________;A点表示________;B点表示________.
(2)从图中可知,小明家离体育馆________m,父子俩在出发后________
 相遇.
相遇.(3)你能求出父亲与小明相遇时距离体育馆还有多远?
(4)小明能否在比赛开始之前赶回体育馆?
-
科目: 来源: 题型:
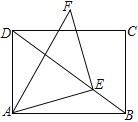
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,E为对角线BD上一个动点,以E为直角顶点,AE为直角边作等腰Rt△AEF,A、E、F按逆时针排列.当点E从点B运动到点D时,点F的运动路径长为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积为______。

相关试题

