【题目】问题探究:探究与应用
(1)如图1,在正方形ABCD中,AB=2,点E是边AD的中点,请在对角线AC上找一点P,使得PE+PD的值最小,并求出这个最小值;(不用写作法,保留作图痕迹)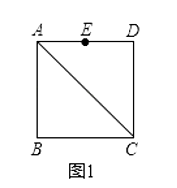
(2)如图2,在矩形ABCD中,AB=6,BC=8,点E是边BC的中点,若点P是边AB上一动点,当△PED的周长最小时,求BP的长度;
问题解决:
(3)某市规划在市中心广场内修建一个矩形的活动中心,如图3,矩形OABC是它的规划图纸,其中A为入口,已知OA=30,OC=20,点E是边AB的中点,以顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系,点D是边OA上一点,若将△ABD沿BD翻折,点A恰好落在边BC上的点F处,在点F处设一出口,点M、N分别是边OA、OC上的点,现规划在点M、N、F、E四处各安置一个健身器材,并依次修建MN、NF、FE及EM四条小路,则是否存在点M、N,使得这四条小路的总长度最小?若存在,求出这个最小值;若不存在,请说明理由.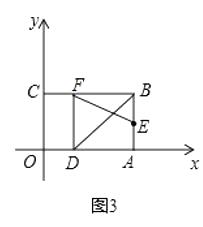
参考答案:
【答案】
(1)解:连接BE交AC于P,如图1所示:

则点P即为所求,
∴此时BE的长就是PE+PD的最小值,
∵在正方形ABCD中,AB=2,点E是边AD的中点,
∴AD=AB=2,AE=DE= ![]() AD=1,PE+PD=BE=
AD=1,PE+PD=BE= ![]() =
= ![]() ;
;
即PE+PD的最小值为 ![]()
(2)解:作点E关于直线AB的对称点E',连接DE',交AB于点P,连接PE、DE,如图2所示:
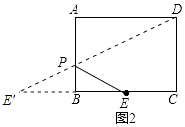
则此时△PED的周长最小,
∵在矩形ABCD中,AB=6,BC=8,点E是边BC的中点,
∴∠PBE'=∠C=90°,CD=AB=6,BE'=BE= ![]() BC=4,
BC=4,
又∵∠E'=∠E',
∴△PBE'∽△DCE',
∴ ![]() ,即
,即 ![]() ,
,
解得:BP=2,
即当△PED的周长最小时,BP的长度为2
(3)解:作点E关于x轴的对称点E',作点F关于y轴的对称点F',连接E'F',与x轴、y轴分别交于点M、N,连接MN、NF、FE、EM,如图3所示:
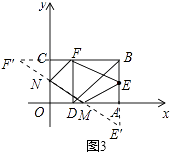
则此时这四条小路的总长最小,且最小值为E'F'+EF的长,
由题意得:BC=OA=30,AB=OC=20,点E为AB中点,
∴AE'=AE=BE= ![]() AB=10,
AB=10,
∴E(30,10),E'(30,﹣10),
由折叠的性质得:BF=AB=20,
∴CF'=CF=30﹣20=10,
∴F'(10,20),F'(﹣10,20),
∴EF= ![]() =10
=10 ![]() ,
,
在Rt△BE'F'中,BF'=BC+CF'=40,BE'=AB+AE'=30,
∴E'F'= ![]() =50,
=50,
由对称的性质得:MN+NF+FE+EM=E'F'+EF=50+10 ![]() ,
,
即存在点M、N,使得这四条小路的总长度最小,这个最小值为50+10 ![]() .
.
【解析】(1)解决“两条线段之和最小值”的基本方法为对称法;(2)利用对称法,作出E关于直线AB的对称点E',连接DE',交AB于点P,可证出△PBE'∽△DCE',对应边成比例列出方程,求出BP;(3)四条线段的和最小值仍可采用对称法,转化为两条线段之和,即作点E关于x轴的对称点E',作点F关于y轴的对称点F',连接E'F',与x轴、y轴分别交于点M、N,再由折叠的性质和勾股定理可求出结果.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.

小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
-
科目: 来源: 题型:
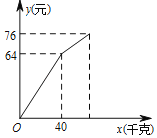
查看答案和解析>>【题目】小华在暑假社会实践过程中,以每千克0.5元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示,请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的关系式?
(2)小华从批发市场共购进多少千克西瓜?
(3)小华这次卖瓜赚了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:

(1)B出发时与A相距 千米.
(2)B骑车一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程y与时间x的函数关系式.(写出过程)
(5)若B的自行车不发生故障,保持出发时的速度匀速行驶,A,B肯定会提前相遇.在图中画出这种假设情况下B骑车行驶过程中路程y与时间x的函数图象,在图中标出这个相遇点P,并回答相遇点P离B的出发点O相距多少千米.(写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的函数解析式为y=2x–2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组
 的解.
的解.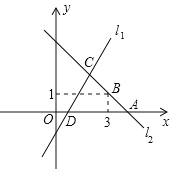
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面内的直线有相交和平行两种位置关系.
(1)如图(a),已知AB∥CD,求证:∠BPD=∠B+∠D.
(2)如图(b),已知AB∥CD,求证:∠BOD=∠P+∠D.
(3)根据图(c),试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.
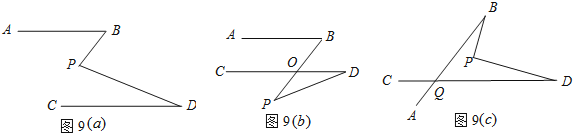
相关试题

