【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

参考答案:
【答案】(1)见解析;(2)18°.
【解析】试题分析:(1)先由对角线互相平分证明四边形ABCD是平行四边形,再由对角互补得出∠ABC=90°,即可得出结论;
(2)先求出∠FDC=36°,再求出∠DCO=54°,然后求出∠ODC=54°,即可求出∠BDF.
试题解析:
(1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴OC=OD,
∴∠ODC=54°
∴∠BDF=∠ODC﹣∠FDC=18°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 三角形的内心到三角形三个顶点的距离相等
B. 三点确定一个圆
C. 平分弦的直径垂直于弦
D. 同圆或等圆中,相等的弧所对的圆心角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x。

(1)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由;
(2)当x为何值时,点P到点A的距离等于点P到点B的距离的2倍?
(3)当x=2时,点A以2个单位长度/秒的速度向左运动,同时点B以1个单位长度/秒向右运动, 问多长时间后点P到点A,点B的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于1而小于4的整数有_________个;已知点A在数轴上表示的数是-2,则与点A的距离等于3的点表示的数是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(1)(-2)+(+10); (2)
 ;
;(3)(-0.5)-|-2.5|; (4) 2+(-7)-(-13;
(5)
 ; (6)
; (6) ;
;(7)
 ; (8)
; (8) ;
;(9)
 ; (10)
; (10) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若am=8,an=2,则am﹣2n的值等于( )
A.1
B.2
C.4
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
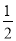 x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A,点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在平面内,以线段MN为对角线作正方形MPNQ,请直接写出点Q的坐标.
相关试题

