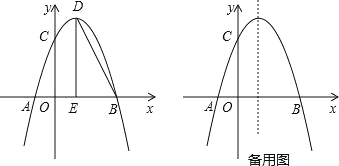
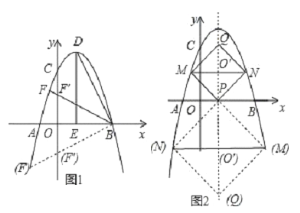
【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A，点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．

（1）求抛物线的解析式及点D的坐标；

（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；

（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在平面内，以线段MN为对角线作正方形MPNQ，请直接写出点Q的坐标．

参考答案：

【答案】（1）y=﹣x2+2x+6，D（2，8）；（2）点F的坐标为（﹣1，）或（﹣3，﹣）；（3）点Q的坐标为（2，﹣1）或（2，﹣﹣1）．

【解析】

试题分析：（1）由点B、C的坐标利用待定系数法即可求出抛物线的解析式，再利用配方法将抛物线解析式变形成顶点式即可得出结论；（2）设线段BF与y轴交点为点F′，设点F′的坐标为（0，m），由相似三角形的判定及性质可得出点F′的坐标，根据点B、F′的坐标利用待定系数法可求出直线BF的解析式，联立直线BF和抛物线的解析式成方程组，解方程组即可求出点F的坐标；（3）设对角线MN、PQ交于点O′，如图2所示．根据抛物线的对称性结合正方形的性质可得出点P、Q的位置，设出点Q的坐标为（2，2n），由正方形的性质可得出点M的坐标为（2﹣n，n）．由点M在抛物线图象上，即可得出关于n的一元二次方程，解方程可求出n值，代入点Q的坐标即可得出结论．

试题解析：（1）将点B（6，0）、C（0，6）代入y=﹣x2+bx+c中，

得：，解得：，

∴抛物线的解析式为y=﹣x2+2x+6．

∵y=﹣x2+2x+6=﹣（x﹣2）2+8，

∴点D的坐标为（2，8）．

（2）设线段BF与y轴交点为点F′，设点F′的坐标为（0，m），如图1所示．

∵∠F′BO=∠FBA=∠BDE，∠F′OB=∠BED=90°，

∴△F′BO∽△BDE，

∴．

∵点B（6，0），点D（2，8），

∴点E（2，0），BE=6﹣4=4，DE=8﹣0=8，OB=6，

∴OF′=OB=3，

∴点F′（0，3）或（0，﹣3）．

设直线BF的解析式为y=kx±3，

则有0=6k+3或0=6k﹣3，

解得：k=﹣或k=，

∴直线BF的解析式为y=﹣x+3或y=x﹣3．

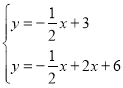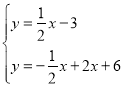联立直线BF与抛物线的解析式得：①或②，

解方程组①得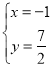：或（舍去），

∴点F的坐标为（﹣1，）；

解方程组②得：或（舍去），

∴点F的坐标为（﹣3，﹣）．

综上可知：点F的坐标为（﹣1，）或（﹣3，﹣）．

（3）设对角线MN、PQ交于点O′，如图2所示．

∵点M、N关于抛物线对称轴对称，且四边形MPNQ为正方形，

∴点P为抛物线对称轴与x轴的交点，点Q在抛物线对称轴上，

设点Q的坐标为（2，2n），则点M的坐标为（2﹣n，n）．

∵点M在抛物线y=﹣x2+2x+6的图象上，

∴n=﹣（2-n）2+2（2﹣n）+6，即n2+2n﹣16=0，

解得：n1=﹣1，n2=﹣﹣1．

∴点Q的坐标为（2，﹣1）或（2，﹣﹣1）．

关闭