【题目】学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60
参考答案:
【答案】B
【解析】解:∵共有18名同学,
则中位数为第9名和第10名同学成绩的平均分,即中位数为: ![]() =9.60,
=9.60,
众数为:9.60.
故B符合题意.
所以答案是:B.
【考点精析】本题主要考查了中位数、众数的相关知识点,需要掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象的一支位于第一象限.
的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于
 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形OABC的边OC、OA分别在x、y轴的正半轴上,点B坐标为(10,10),点P从O出发沿O→C→B运动,速度为1个单位每秒,连接AP.设运动时间为t.

(1)若抛物线y=﹣(x﹣h)2+k经过A,B两点,求抛物线函数关系式;
(2)当0≤t≤10时,如图1,过点O作OH⊥AP于点H,直线OH交边BC于点D,连接AD,PD,设△APD的面积为S,求S的最小值;
(3)在图2中以A为圆心,OA长为半径作⊙A,当0≤t≤20时,过点P作PQ⊥x轴(Q在P的上方),且线段PQ=t+12:
①当t在什么范围内,线段PQ与⊙A只有一个公共点?当t在什么范围内,线段PQ与⊙A有两个公共点?
②请将①中求得的t的范围作为条件,证明:当t取该范围内任何值时,线段PQ与⊙A总有两个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期学习了一元一次方程的解法,下面是林林同学的解题过程:解方程
 =1
=1解:方程两边同时乘以6,得:
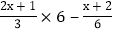 ×6=1×6…………第①步
×6=1×6…………第①步去分母,得:2(2x+1)-x+2=6………………第②步
去括号,得:4x+2-x+2=6…………………第③步
移项,得:4x-x=6-2-2…………………第④步
合并同类项,得:3x=2…………………………第⑤步
系数化1,得:x=
 …………………………第⑥步
…………………………第⑥步上述林林的解题过程从第______步开始出现错误,错误的原因是______.
请你帮林林改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)﹣7+(﹣8)﹣(﹣18)﹣13
(2)(﹣1)3×(﹣5)﹣(﹣3)÷(﹣
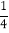 )
)(3)(
 -
-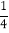 -
-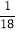 )÷(﹣
)÷(﹣ )
)(4)﹣12018﹣2
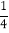 ×[13﹣(﹣5)2]
×[13﹣(﹣5)2] -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
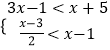 并写出它的整数解.
并写出它的整数解.
相关试题

