【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0;②c>0;③b2﹣4ac>0;④a﹣b+c<0,其中正确的个数有( ) 
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:①∵抛物线开口向下,∴a<0,而对称轴在y轴左侧,∴a、b同号,即b<0,正确; ②∵抛物线与y轴的交点在正半轴,∴c>0,正确;
③∵图象与x轴有两个交点,∴b2﹣4ac>0,正确;
④∵由图象可知当x=﹣1时,对应的函数值y=a﹣b+c>0,错误.
故选C.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
2.5
余油量y(升)
100
80
60
50
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.

(1)求证:AC平分∠DAB;
(2)若⊙O的半径为5,且tan∠DAC= ,求BC的长.
,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元?
(2)若体育老师带了6000元去购买这种篮球与足球共80个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+
x2+  x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.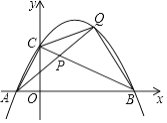
(1)①写出点A,B,C的坐标:A(),B(),C();
②求证:△ABC是直角三角形;
(2)记△BCQ的面积为S,求S关于x的函数表达式;
(3)在点P的运动过程中,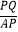 是否存在最大值?若存在,求出
是否存在最大值?若存在,求出 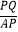 的最大值及点Q的坐标;若不存在,请说明理由.
的最大值及点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣18×(﹣2)÷3
(2)(﹣
 )×(﹣90)÷
)×(﹣90)÷
(3)﹣2.5÷
 ×(﹣
×(﹣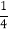 );
);(4)(﹣10)2﹣[16+(﹣3)2]
(5)(
 ﹣
﹣ +2)÷
+2)÷
相关试题

