【题目】如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD=9,AE⊥BC于E,AE=8,则CD的长为_____.
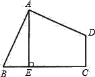
参考答案:
【答案】8﹣![]()
【解析】
作DF⊥AE于F,则四边形DCEF为矩形,即DC=EF,要求CD的长度,求出AF即可.再根据△ABE≌△ADF,要求AF求出BE即可.
如图,
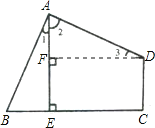
作DF⊥AE于F,则DCEF为矩形,DC=EF,
又∵∠1+∠2=90°,
∠2+∠3=90°,
∴∠1=∠3,
又∵AB=AD,
∴△ABE≌△ADF,
∴AF=BE,
在Rt△ABE中,
BE=![]() ,
,
∴DC=EF=AE-AF=8-![]() .
.
故答案为:8﹣![]() .
.
点睛】本题考查了在直角三角形中勾股定理的合理运用和全等三角形的构建及证明.解本题关键是求证全等三角形,和已知2边求直角三角形的第3边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并直接写出此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .
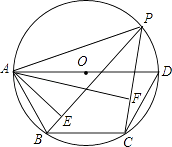
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣3|﹣(2016+sin30°)0﹣(﹣
 )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
相关试题

