【题目】如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积.

参考答案:
【答案】图中阴影部分的面积为![]() .
.
【解析】试题分析:
如图,设点C在BD上的对应点为点F,连接EF,则易得EF⊥BD于点F,BF=BC=12,由已知易得BD=13,由此可得DF=1,设CE=x,则EF=x,DE=5-x,在Rt△DEF中由勾股定理建立方程即可求得x的值,从而可得到EF的长,结合BD的长即可求出△BDE的面积了.
试题解析:
设折叠后点C在BD上的对应点为点F,连接EF,
∴EF⊥BD,BF=BC=12,
∴∠DFE=90°,
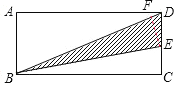
∵AB=5,AD=BC=12,∠A=90°,
∴BD=![]() ,
,
∴DF=13-12=1,
设CE=x,则EF=CE=x,DE=5-x,
在△DEF中,x2+12=(5-x)2,
解得x=![]() ,
,
∴图中阴影部分的面积S△BDE=![]() ×13×
×13×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.

-
科目: 来源: 题型:
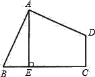
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD=9,AE⊥BC于E,AE=8,则CD的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|﹣3|﹣(2016+sin30°)0﹣(﹣
 )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几? -
科目: 来源: 题型:
查看答案和解析>>【题目】一驾2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远(其中梯子从AB位置滑到CD位置)?
-
科目: 来源: 题型:
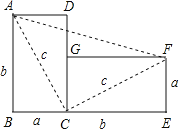
查看答案和解析>>【题目】如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
相关试题

