【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并直接写出此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?

参考答案:
【答案】(1)全等。理由见解析;(2)S=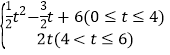 ;(3)点Q运动的速度为=3÷2=1.5cm/秒时,△AEP≌△BQP..
;(3)点Q运动的速度为=3÷2=1.5cm/秒时,△AEP≌△BQP..
【解析】
(1)本题很容易证明△AEP≌△BPQ,这样可得出∠AEP=∠BPQ,因为∠AEP+∠APE=90°,可得出∠BPQ+∠APE=90°,这即可判断出结论.
(2)可分别用t表示出AP、BQ、BP的长度,然后用梯形的面积减去△APE、△BPQ的面积即可得出△PEQ的面积为Scm2.
(3)设Q运动的速度为xcm/s,则根据△AEP与△BQP得出AP=BP、AE=BQ,解出即可得出答案.
(1)全等,
理由:当t=1时,AP=1,BQ=1,∴AP=BQ.
∵E是AD的中点,∴![]()
∵PB=AB=AP=4﹣1=3,∴AE=PB.
在Rt△EAP和Rt△PBQ中,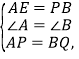
∴△EAP≌Rt△PBQ(SAS).
此时![]() .
.
(2)如图1所示连接QE.
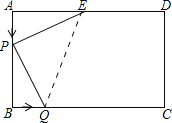
图1
当t≤4时,AP=BQ=t,
S梯形AEQB![]()
![]()
![]()
∴![]()
如图2所示:
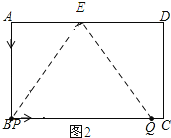
当4<t≤6时,点P与点B重合,
![]()
∴S与t的函数关系式为S=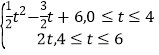 ;
;
(t的取值范围不做要求)
(3)如图3所示:
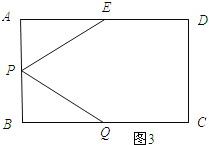
∵△AEP≌△BQP,PA≠BQ,
∴AP=PB=2,AE=BQ=3.
∴![]()
∴点Q运动的速度为=3÷2=1.5cm/秒时,△AEP≌△BQP..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )

A.90° B.120° C.135° D.150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.

(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .
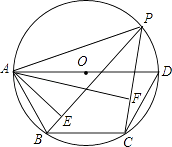
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD=9,AE⊥BC于E,AE=8,则CD的长为_____.
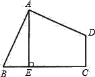
相关试题

