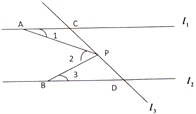
【题目】如图,已知直线![]() ,直线
,直线![]() 和直线交于点
和直线交于点![]() 和点
和点![]() ,
,![]() 为直线
为直线![]() 上的一点,
上的一点,![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上的定点.
上的定点.
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动时,问
两点除外)上运动时,问![]() 、
、![]() 、
、![]() 之间的关系是什么?这种关系是否发生变化?请说明理由;
之间的关系是什么?这种关系是否发生变化?请说明理由;
(2)若![]() 在线段
在线段![]() 之外时,
之外时,![]() 、
、![]() 、
、![]() 的关系又怎样?说明理由.
的关系又怎样?说明理由.
参考答案:
【答案】(1)![]() ,不变化,理由见解析;(2)在
,不变化,理由见解析;(2)在![]() 上面时,
上面时,![]() ,在
,在![]() 下面时,
下面时,![]() ,理由见解析.
,理由见解析.
【解析】
(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,故可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)由于点P的位置不确定,故应分当点P在![]() 上面时与点P在
上面时与点P在![]() 下面时两种情况进行讨论.
下面时两种情况进行讨论.
(1)∠2=∠1+∠3.
证明:如图1,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;
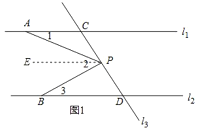
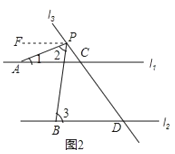
(2)①如图2所示,当点P在![]() 上面时,∠2=∠3∠1,
上面时,∠2=∠3∠1,
理由:过点P作PF∥l1,∠FPA=∠1.
∵l1∥l2,
∴PF∥l2,
∴∠FPB=∠3,
∴∠2=∠FPB∠PFA=∠3∠1;
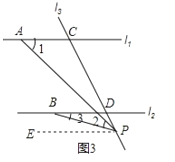
②如图3所示,当点P在![]() 下面时,∠2=∠1∠3,
下面时,∠2=∠1∠3,
理由:过点P作PE∥l2,∠EPB=∠3.
∵l1∥l2,
∴PE∥l1,
∴∠EPA=∠1,
∴∠2=∠EPA∠EPB=∠1∠3.
-
科目: 来源: 题型:
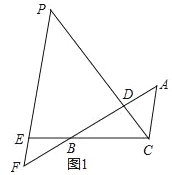
查看答案和解析>>【题目】如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由;
(2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.

-
科目: 来源: 题型:
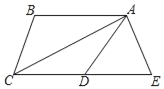
查看答案和解析>>【题目】如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;
(2)若AE=5,AC=12,求线段CE的长;
(3)在(2)的条件下,若线段CD上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两点A、B.
(1)画出符合要求的图形
①画线段AB;
②延长线段AB到点C,使BC=AB;
③反向延长线段AB到点D,使DA=2AB;
④分别取BC、AD的中点M、N.
(2)在(1)的基础上,已知线段AB的长度是4cm,求线段MN的长度.

-
科目: 来源: 题型:
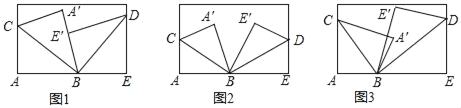
查看答案和解析>>【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中有两种移动电话计费方式:
月使用费(元)
主叫限定时间(分钟)
主叫超时费(元/分钟)
被叫
方式一
65
160
0.25
免费
方式二
100
380
0.19
免费
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
相关试题

