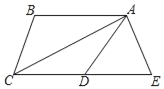
【题目】如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;
(2)若AE=5,AC=12,求线段CE的长;
(3)在(2)的条件下,若线段CD上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.
参考答案:
【答案】(1)证明见解析(2)13(3)![]()
【解析】
(1)由AC平分∠BAD,得到∠BAC=∠DAC,等量代换得到∠BAC=∠ACD,根据平行线的判定定理即可得到结论;
(2)根据等腰三角形的性质得到∠DAE=∠E,根据三角形的内角和得到∠CAE=90°,根据勾股定理得到CE=![]() =
=![]() =13;
=13;
(3)根据三角形的面积公式即可得到结论.
(1)∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DCA=∠CAD,
∴∠BAC=∠ACD,
∴AB∥CD;
(2)∵DE=DA,
∴∠DAE=∠E,
∴∠ACD+∠E=∠CAD+∠DAE=![]() ×180°=90°,
×180°=90°,
∴∠CAE=90°,
∴CE=![]() =
=![]() =13;
=13;
(3)∵AD=CD=DE=![]() ,
,
∵点P在线段CD上,△DPA的面积是△ACD面积的六分之一,
∴PD:CD=![]() ,
,
∴![]() =
=![]() ,
,
∴PC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造
 个新公共自行车站点和配置
个新公共自行车站点和配置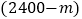 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变) -
科目: 来源: 题型:
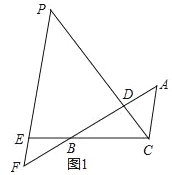
查看答案和解析>>【题目】如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由;
(2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知两点A、B.
(1)画出符合要求的图形
①画线段AB;
②延长线段AB到点C,使BC=AB;
③反向延长线段AB到点D,使DA=2AB;
④分别取BC、AD的中点M、N.
(2)在(1)的基础上,已知线段AB的长度是4cm,求线段MN的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
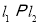 ,直线
,直线 和直线交于点
和直线交于点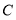 和点
和点 ,
, 为直线
为直线 上的一点,
上的一点,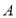 ,
,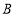 分别是直线
分别是直线 ,
,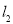 上的定点.
上的定点.(1)若
 点在线段
点在线段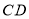 (
(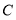 、
、 两点除外)上运动时,问
两点除外)上运动时,问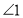 、
、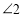 、
、 之间的关系是什么?这种关系是否发生变化?请说明理由;
之间的关系是什么?这种关系是否发生变化?请说明理由;(2)若
 在线段
在线段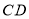 之外时,
之外时,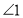 、
、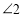 、
、 的关系又怎样?说明理由.
的关系又怎样?说明理由.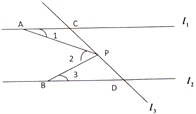
-
科目: 来源: 题型:
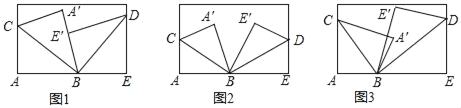
查看答案和解析>>【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
相关试题

