【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC. 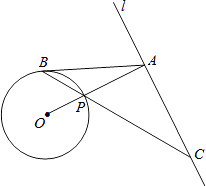
(1)求证:AB是⊙O的切线;
(2)PC=2 ![]() ,OA=4. ①求⊙O的半径;
,OA=4. ①求⊙O的半径;
②求线段PB的长.
参考答案:
【答案】
(1)证明:连结OB,如图,
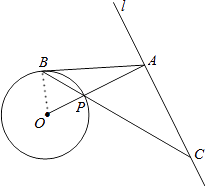
∵AB=AC,
∴∠1=∠2,
∵OA⊥AC,
∴∠2+∠3=90°,
∵OB=OP,
∴∠4=∠5,
而∠3=∠4,
∴∠5+∠2=90°,
∴∠5+∠1=90°,即∠OBA=90°,
∴OB⊥AB,
∴AB是⊙O的切线;
(2)解:①作OH⊥PB于H,如图,则BH=PH,
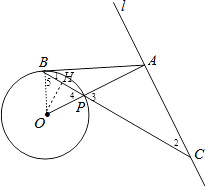
设⊙O的半径为r,则PA=OA﹣OP=4﹣r,
在Rt△PAC中,AC2=PC2﹣PA2=(2 ![]() )2﹣(4﹣r)2,
)2﹣(4﹣r)2,
在Rt△OAB中,AB2=OA2﹣OB2=42﹣r2,
而AB=AC,
∴(2 ![]() )2﹣(4﹣r)2=42﹣r2,解得r=1,
)2﹣(4﹣r)2=42﹣r2,解得r=1,
即⊙O的半径为1;
②∵⊙O的半径为1
∴PA=3,
∵∠3=∠4,
∴Rt△APC∽Rt△HPO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PH= ![]() ,
,
∴PB=2PH= ![]() .
.
【解析】(1)连结OB,如图,由等腰三角形的性质得∠1=∠2,∠4=∠5,由OA⊥AC得∠2+∠3=90°,加上∠3=∠4,易得∠5+∠1=90°,即∠OBA=90°,于是根据切线的判定定理可得AB是⊙O的切线;(2)作OH⊥PB于H,如图,根据垂径定理得到BH=PH,设⊙O的半径为r,则PA=OA﹣OP=4﹣r,根据勾股定理得到AC,AB,然后根据相似三角形的性质即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知数轴上点A表示的数为8,B是数轴上一点,且AB=22.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数____,点P表示的数____(用含t的代数式表示);
(2)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(列一元一次方程解应用题)
(3)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问 秒时P、Q之间的距离恰好等于2(直接写出答案)
(4)思考在点P的运动过程中,若M为AP的中点,N为PB的中点.线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.

-
科目: 来源: 题型:
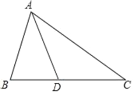
查看答案和解析>>【题目】如图,在△ABC中,点D在AC的垂直平分线上.
(1)若AB=AD,∠BAD=26°,求∠B和∠C的度数;
(2)若AB=AD=DC,AC=BC,求∠C的度数;
(3)若AC=6,△ABD的周长为13cm,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x
销售量y(件)
销售玩具获得利润w(元)
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具车规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌服装获得的最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】求一个正数的算术平方根,有些数可以直接求得,如
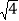 ;有些数则不能直接求得,如
;有些数则不能直接求得,如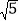 ,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:
,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:n
0.09
9
900
90000
…
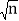
0.3
3
30
300
…
(1)根据表中的规律,可以求得
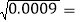 ____,
____,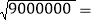 ____;
____;(2)根据表中的规律,还可以由
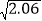 ≈1.435,求得
≈1.435,求得 ≈____,
≈____,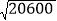 ≈____,
≈____,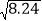 ≈____.
≈____. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=﹣1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(﹣1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k﹣1)的图象是“点选直线”
(1)一次函数y=(k+3)x+(k﹣1)的图象经过的顶点P的坐标是 .
(2)已知一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
-
科目: 来源: 题型:
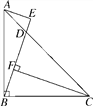
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
相关试题

