【题目】如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm

(1)填空:AD= (cm),DC= (cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=![]() ,sin15°=
,sin15°=![]() )
)
参考答案:
【答案】(1)![]() ;
;![]() ;
;
(2)![]() ;
;
(3)![]()
【解析】
试题分析:(1)由勾股定理求出AC,由∠CAD=30°,得出DC=![]() AC=
AC=![]() ,由三角函数求出AD即可;
,由三角函数求出AD即可;
(2)过N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,则NE=DF,求出∠NCF=75°,∠FNC=15°,由三角函数求出FC,得NE=DF=![]() x
x![]() ,即可得出结果;
,即可得出结果;
(3)由三角函数求出FN,得出PF,△PMN的面积y=梯形MDFN的面积﹣△PMD的面积﹣△PNF的面积,得出y是x的二次函数,即可得出y的最大值.
试题解析:(1)∵∠ABC=90°,AB=BC=4cm,
∴AC=![]() =
=![]() =
=![]() ,
,
∵∠ADC=90°,∠CAD=30°,
∴DC=![]() AC=
AC=![]() ,
,
∴AD=![]() DC=
DC=![]() ;
;
故答案为:![]() ;
;![]()
(2)过点N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,如图所示:
则NE=DF,
∵∠ABC=∠ADC=90°,AB=BC,∠CAD=30°,
∴∠ACB=45°,∠ACD=60°,
∴∠NCF=180°﹣45°﹣60°=75°,∠FNC=15°,
∵sin∠FNC=![]() ,NC=x,
,NC=x,
∴FC=![]() x,
x,
∴NE=DF=![]()
∴点N到AD的距离为![]()
(3)∵sin∠NCF=![]() ,
,
∴FN=![]() x,
x,
∵P为DC的中点,
∴PD=CP=![]() ,
,
∴PF=![]() x+
x+![]() ,
,
∴△PMN的面积y=梯形MDFN的面积﹣△PMD的面积﹣△PNF的面积
=![]() (
(![]() x+
x+![]() ﹣x)(
﹣x)(![]() x+2
x+2![]() )﹣
)﹣![]() (
(![]() ﹣x)×
﹣x)×![]() ﹣
﹣![]() (
(![]() x+
x+![]() )(
)(![]() x)
x)
=![]()
即y是x的二次函数,
∵![]() <0,
<0,
∴y有最大值,
当x=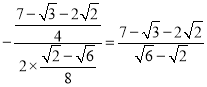 时,
时,
y有最大值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图在平面直角坐标系xOy中,矩形OABC的边OA在y轴的负半轴上,OC在x轴的正半轴上,OA=2,OC=3,过原点O作∠AOC的平分线交线段AB于点D,连接DC,过点D作DE⊥DC,交线段OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)如图2将∠EDC绕点D按逆时针方向旋转后,角的一边与y轴的负半轴交于点F,另一边与线段OC交于点G,如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
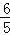 ,求证:EF=2GO;
,求证:EF=2GO;(3)对于(2)中的点G,在位于第四象限内的该跑物像上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
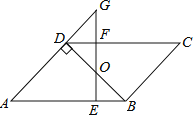
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )

A. ①② B. ③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直径AB=5cm的圆上,到AB的距离为2.5cm的点有( )
A. 无数个 B. 1个 C. 2个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班分两组志愿者去社区服务,第一组20人,第二组26人.现第一组发现人手不够,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A. 20=2(26﹣x) B. 20+x=2×26 C. 2(20+x)=26﹣x D. 20+x=2(26﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】桥梁上的拉杆,电视塔的底座,都是三角形结构,而活动挂架是四边形结构,这是分别利用三角形和四边形的________________________________.
相关试题

