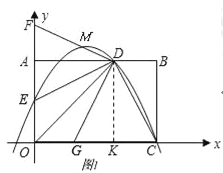
【题目】已知:如图在平面直角坐标系xOy中,矩形OABC的边OA在y轴的负半轴上,OC在x轴的正半轴上,OA=2,OC=3,过原点O作∠AOC的平分线交线段AB于点D,连接DC,过点D作DE⊥DC,交线段OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)如图2将∠EDC绕点D按逆时针方向旋转后,角的一边与y轴的负半轴交于点F,另一边与线段OC交于点G,如果DF与(1)中的抛物线交于另一点M,点M的横坐标为![]() ,求证:EF=2GO;
,求证:EF=2GO;
(3)对于(2)中的点G,在位于第四象限内的该跑物像上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)EF=2GO;
;(2)EF=2GO;
(3)Q(2,2)或(1,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用待定系数法求解抛物线解析式;
(2)利用待定系数法求解直线解析式,得到F(0,3),EF=2,从而得出∠FDA=∠GDK,KG=AF即可;
(3)分三种情况,①PG=PC,②若PG=GC,③若PG=GC,由勾股定理解得即可.
试题解析:(1)由已知,得C(3,0),D(2,2),
∵∠ADE90°﹣∠CDB=∠BCD,
∴AD=BC,AD=2,
∴E(0,1),设过点E,D,C的抛物线的解析式为y=ax2+bx+c(a≠0),
将点E,D,C的坐标分别代入,得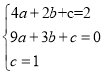 ;
;
解这个方程组,得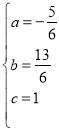 ,
,
∴抛物线点的解析式为![]() ;
;
(2)证明:∵点M在抛物线上,且它的横坐标为![]() ,
,
设DM的解析式为y=kx+m(k≠0),
将点D,M的坐标分别代入,得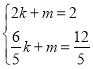 ,
,
解得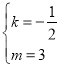 ,
,
∴DM的解析式为![]() ,
,
∴F(0,3),EF=2.
过点D作DK⊥OC于K,
∴DA=DK,
∵∠ADK=∠FDG=90°,
∴∠FDA=∠GDK,
∴KG=AF=1,
∵OC=3,
∴EF=2GO.
(3)如图:
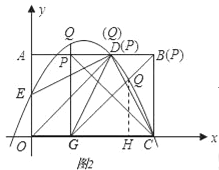
∵点P在AB上,G(1,0),C(3,0),
则设P(t,2),
∴PG2=(t﹣1)2+22,PC2=(3﹣t)2+22,CG=2
①PG=PC,
∴(t﹣1)2+22=(3﹣t)2+22,
∴t=2
∴P(2,2),
此时点Q与点P重合,
∴Q(2,2),
②若PG=GC,
∴(t﹣1)2+22=22,
∴t=1,
∴P(1,2),
此时GP⊥x轴,GP与抛物线在第一象限内的交点Q的横坐标为1,
∴Q的纵坐标为![]() ,
,
∴Q(1,![]() ).
).
③若PG=GC,
∴(3﹣t)2+22=22,
∴t=3,
∴P(3,2),此时PC=GC=2,
∴△PGC为等腰直角三角形,过点Q作QH⊥x轴于点H,
∴QH=GH,SHE QH=h,
∴Q(h+1,h),
∴![]() (h+1)2+
(h+1)2+![]() (h+1)+1=h,
(h+1)+1=h,
∴h=﹣2(舍)或h=![]() ,
,
∴Q(![]() ,
,![]() ),
),
∴Q(2,2)或(1,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,PQ切⊙O于T,AC⊥PQ于C,交⊙O于D.
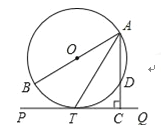
(1)求证:AT平分∠BAC;
(2)若AO=2,AT=
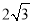 ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
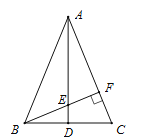
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
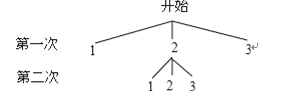
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
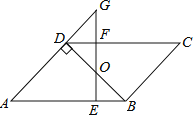
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )

A. ①② B. ③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm

(1)填空:AD= (cm),DC= (cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=
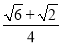 ,sin15°=
,sin15°=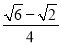 )
)
相关试题

