【题目】如图,在平行四边形ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点.
求证:(1)DE⊥OC;
(2)EG=EF.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由四边形ABCD是平行四边形,AC与BD相交于点O,根据平行四边形的性质,即可得BD=2OD,AB=CD,AD=BC,又由BD=2AB,可得△ODC是等腰三角形,根据三线合一的性质,即可证得DE⊥OC;
(2)由DE⊥OC,点G是AD的中点,利用直角三角形斜边上的中线等于斜边的一半,即可得EG=![]() AD,又由三角形中位线的性质,求得EF=
AD,又由三角形中位线的性质,求得EF=![]() BC,则可证得EG=EF.
BC,则可证得EG=EF.
试题解析:(1)∵四边形ABCD是平行四边形,AC与BD相交于点O,
∴BD=2OD,AB=CD,AD=BC.
∵BD=2AB,
∴OD=AB=CD.
∵点E是OC的中点,
∴DE⊥OC.
(2)∵DE⊥OC,点G是AD的中点,
∴EG=![]() AD;
AD;
∵点E、F分别是OC、OB的中点.
∴EF=![]() BC.
BC.
∵AD=BC,
∴EG=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,﹣1)与反比例函数y=
 在第一象限内的图象交于点C,点C的纵坐标为1.
在第一象限内的图象交于点C,点C的纵坐标为1. 
(1)求一次函数的解析式;
(2)求点C的坐标及反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一张边长为4的正方形纸片
 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:

(1)△ODE≌△FCE;
(2)四边形ODFC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
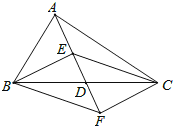
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
相关试题

