【题目】计算或化简:
(1)2﹣1+![]()
(2)2x2y(﹣3xy)÷(xy)2
(3)(﹣2a)(3a2﹣a+3)
(4)(x+3)(x+4)﹣(x﹣1)2
(5)[2a3x2(a﹣2x)﹣![]() a2x2]÷(﹣ax)2
a2x2]÷(﹣ax)2
参考答案:
【答案】(1)![]() ;(2)﹣6x;(3)﹣6a3+2a2﹣6a;(4)9x+11;(5)2a2﹣4ax﹣
;(2)﹣6x;(3)﹣6a3+2a2﹣6a;(4)9x+11;(5)2a2﹣4ax﹣![]()
【解析】
(1)实数的混合运算,先分别对负整数指数幂,二次根式,求一个数的立方根和零指数幂进行化简,然后再计算;
(2)整式的乘除混合运算,先做乘方,然后再做乘除;
(3)用单项式乘多项式的法则进行计算;
(4)整式的加减乘除混合运算,先做乘方,然后做多项式乘法,然后再去括号,进行合并同类项计算;
(5)整式的加减乘除混合运算,先做乘方,然后做乘除,最后做加减.
解:(1)2﹣1+![]()
=![]()
=![]() ;
;
(2)2x2y(﹣3xy)÷(xy)2
=﹣6x3y2÷x2y2
=﹣6x;
(3)(﹣2a)(3a2﹣a+3)=﹣6a3+2a2﹣6a;
(4)(x+3)(x+4)﹣(x﹣1)2
=x2+7x+12﹣(x2﹣2x+1)
= x2+7x+12﹣x2+2x-1
=9x+11;
(5)[2a3x2(a﹣2x)﹣![]() a2x2]÷(﹣ax)2
a2x2]÷(﹣ax)2
=(2a4x2﹣4a3x3﹣![]() a2x2)÷(a2x2),
a2x2)÷(a2x2),
=2a2﹣4ax﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=
 .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
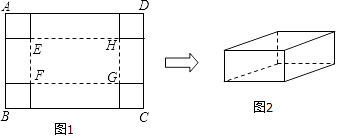
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

