【题目】解方程
(1)x2﹣7x+10=0
(2)3(x﹣2)+x2﹣2x=0.
参考答案:
【答案】
(1)解:x2﹣7x+10=0,
(x﹣2)(x﹣5)=0,
x1=2,x2=5
(2)解:3(x﹣2)+x2﹣2x=0,
x2+x﹣6=0,
(x+3)(x﹣2)=0,
x1=﹣3,x2=2
【解析】(1)根据十字相乘法把要求的式子进行因式分解,得到两个一元一次方程的解,然后求解即可;(2)先把给出的方程进行整理,得到方程x2+x﹣6=0,再因式因式分解,即可得出答案.
【考点精析】解答此题的关键在于理解因式分解法的相关知识,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个二次函数的图象顶点坐标为(2,1),形状与抛物线y=﹣2x2相同,试写出这个函数解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】中心对称图形和旋转对称图形的区别是什么呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. ﹣3(a﹣b)=﹣3a﹣b B. ﹣3(a﹣b)=﹣3a+b
C. ﹣3(a﹣b)=﹣3a﹣3b D. ﹣3(a﹣b)=﹣3a+3b
-
科目: 来源: 题型:
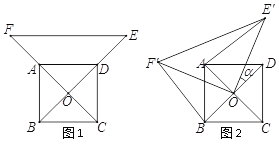
查看答案和解析>>【题目】如图1,已知
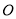 为正方形
为正方形 的中心,分别延长
的中心,分别延长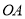 到点
到点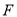 ,
, 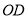 到点
到点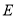 ,使
,使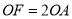 ,
, 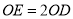 ,连结
,连结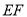 ,将△
,将△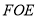 绕点
绕点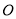 逆时针旋转
逆时针旋转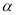 角得到△
角得到△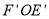 (如图2).连结
(如图2).连结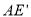 、
、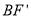 .
.
(Ⅰ)探究
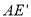 与
与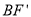 的数量关系,并给予证明;
的数量关系,并给予证明;(Ⅱ)当
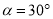 ,
, 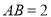 时,求:
时,求:①
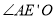 的度数;
的度数;②
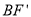 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
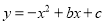 与
与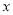 轴交于
轴交于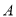 、
、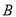 两点(点
两点(点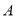 在点
在点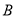 的左侧),点
的左侧),点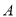 的坐标为
的坐标为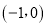 ,与
,与 轴交于点
轴交于点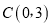 ,作直线
,作直线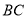 .动点
.动点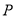 在
在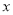 轴上运动,过点
轴上运动,过点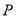 作
作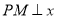 轴,交抛物线于点
轴,交抛物线于点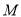 ,交直线
,交直线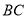 于点
于点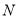 ,设点
,设点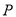 的横坐标为
的横坐标为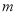 .
.(Ⅰ)求抛物线的解析式和直线
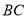 的解析式;
的解析式;(Ⅱ)当点
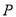 在线段
在线段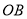 上运动时,求线段
上运动时,求线段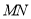 的最大值;
的最大值;(Ⅲ)当以
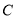 、
、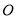 、
、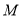 、
、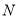 为顶点的四边形是平行四边形时,直接写出
为顶点的四边形是平行四边形时,直接写出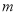 的值.
的值.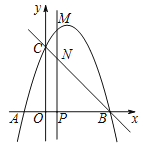
-
科目: 来源: 题型:
查看答案和解析>>【题目】全等的两个图形一定关于中心对称吗?
相关试题

