【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
参考答案:
【答案】(1)![]() ;(2)当天销售单价所在的范围为
;(2)当天销售单价所在的范围为![]() ;(3)每件文具售价为9元时,最大利润为280元.
;(3)每件文具售价为9元时,最大利润为280元.
【解析】
(1)根据总利润=每件利润×销售量,列出函数关系式,
(2)由(1)的关系式,即![]() ,结合二次函数的性质即可求
,结合二次函数的性质即可求![]() 的取值范围
的取值范围
(3)由题意可知,利润不超过![]() 即为利润率=(售价-进价)÷售价,即可求得售价的范围.再结合二次函数的性质,即可求.
即为利润率=(售价-进价)÷售价,即可求得售价的范围.再结合二次函数的性质,即可求.
解:
由题意
(1)![]()
故![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]()
(2)要使当天利润不低于240元,则![]() ,
,
∴![]()
解得,![]()
∵![]() ,抛物线的开口向下,
,抛物线的开口向下,
∴当天销售单价所在的范围为![]()
(3)∵每件文具利润不超过![]()
∴![]() ,得
,得![]()
∴文具的销售单价为![]() ,
,
由(1)得![]()
∵对称轴为![]()
∴![]() 在对称轴的左侧,且
在对称轴的左侧,且![]() 随着
随着![]() 的增大而增大
的增大而增大
∴当![]() 时,取得最大值,此时
时,取得最大值,此时![]()
即每件文具售价为9元时,最大利润为280元
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
年份
2014
2015
2016
2017
2018
动车组发送旅客量a亿人次
0.87
1.14
1.46
1.80
2.17
铁路发送旅客总量b亿人次
2.52
2.76
3.07
3.42
3.82
动车组发送旅客量占比
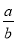 ×100%
×100%34.5%
41.3%
47.6%
52.6%
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用 (填“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为 ,你的预估理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C、E是⊙O上的两点,CE=CB,
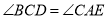 ,延长AE交BC的延长线于点F.
,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF
(3)若BD=1,
 ,求直径AB的长.
,求直径AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,
 .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.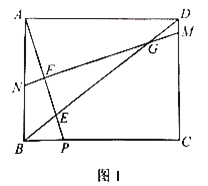
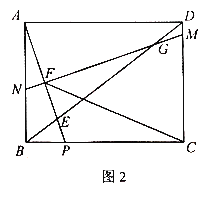
(1)求证:
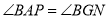 ;
;(2)若
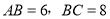 ,求
,求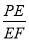 .
.(3)如图2,在(2)的条件下,连接CF,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
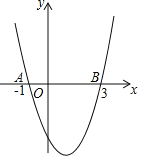
A. ①③ B. ②③ C. ②④ D. ③④
相关试题

