【题目】如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.

参考答案:
【答案】(1)证明见解析(2)3![]()
【解析】试题分析:(1)欲证明△ABD为等腰三角形,只要证明∠DBA=∠DAB即可.
(2)如图2中,只要证明AB是直径即可解决问题.
试题解析:(1)如图1中,

∵CD平分∠EAC,
∴∠ECD=∠DCA,
∵∠ECD=∠DAB,∠DCA=∠DBA,
∴∠DBA=∠DAB,
∴DB=DA.
∵△DBA是等腰三角形.
(2)如图2中,

∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°,
∴AB是直径,
∴∠BDA=90°,
∵BD=AD=6,
∴AB=![]() .
.
∴⊙O的半径为3![]() .
.
-
科目: 来源: 题型:
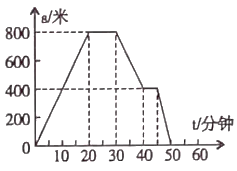
查看答案和解析>>【题目】在周末,小花晚饭后外出散步遇见同学,交谈了一会儿,然后返回,返回途中在报亭看了一会报纸才回到家,如图是根据此情景画出的图象,请回答下列问题:
(1)小花是在距家 米处遇见同学的,交谈了 分钟时间.
(2)报亭离家 米远.
(3)小花在整个过程中走得最快时的速度是 米/分钟.
-
科目: 来源: 题型:
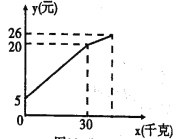
查看答案和解析>>【题目】一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)降价前他每千克萝卜出售的价格是多少?
(2)降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?
-
科目: 来源: 题型:
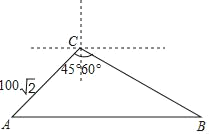
查看答案和解析>>【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100
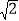 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒. (1)请你帮助他们算一算,这辆小车是否超速?(参考数据:
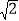 ≈1.41,
≈1.41,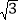 ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
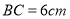 ,将△ABC以每秒2cm的速度沿
,将△ABC以每秒2cm的速度沿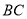 所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使
所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使 成立,则
成立,则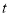 的值为_____秒.
的值为_____秒.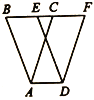
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.

相关试题

