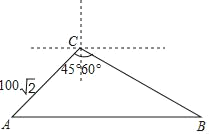
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).
(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
参考答案:
【答案】(1)超速了,理由见解析;(2)答案见解析.
【解析】
(1) 作CD⊥AB于点D,先解等腰直角三角形ADC,得出AD=CD=100,解Rt△BCD中,求出BD≈173,那么AB=AD+BD≈273,再根据速度=路程÷时间得出小轿车经过AB路段的速度,与限制速度相比较即可.
(2)计算出超速的百分比,按交通法规处罚;建议地方公安机关依法严格查处道路交通违法行为和交通事故,指导地方公安机关维护城乡道路交通秩序和公路治安秩序,加强车辆的维护和检查工作.
解:如图,作CD⊥AB于点D.
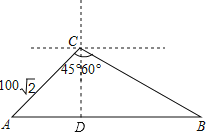
∵在Rt△ADC中,∠ACD=45°,AC=100![]() ,
,
∴CD=ACcos∠ACD=![]() AC=100,
AC=100,
∴AD=CD=100.
∵在Rt△CDB中,∠BCD=60°,
∴∠CBD=30°,
∴BD=![]() CD=100
CD=100![]() .
.
∴AB=AD+BD=100+100![]() =100(
=100(![]() +1)≈273.
+1)≈273.
又∵小轿车经过AB路段用时13秒,
∴小轿车的速度为![]() =21米/秒=75.6千米/时.
=21米/秒=75.6千米/时.
而该路段限速为60千米/时≈16.67米/秒,
∵21>16.67,
∴这辆小轿车超速了.
(2)处理意见: 在限速为50公里以上80公里以下的道路,时速超过限定时速10%以上不到20%的,处100元罚款;超过限定时速20%以上不到50%的,处150元罚款等,因为60×(1+10%)=66千米/时,60×(1+20%)=72千米/时<75.6千米/时<60×(1+50%),所以应该是处150元罚款;因为小车超速未达20%的扣3分,超速20%以上未达到50%的扣6分,所以扣6分.
建议:①地方公安机关依法严格查处道路交通违法行为和交通事故;指导地方公安机关维护城乡道路交通秩序和公路治安秩序,加强车辆的维护和检查工作;②让人民群众认真学习交通安全的法律法规,遵守交通规则,加强安全意识,树立交通安全文明公德,远离伤痛,珍爱生命;③提高驾驶员的职业修养,确确实实牢记安全,在什么样的道路上行驶,都要遵守各种道路的规定,防止疲劳驾车,注意前后车辆的距离等.
-
科目: 来源: 题型:
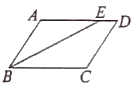
查看答案和解析>>【题目】如图已知BE平分∠ABC,E点在线段AD上,∠ABE=∠AEB,AD与BC平行吗?为什么?
解:因为BE平分∠ABC(已知)
所以∠ABE=∠EBC ( )
因为∠ABE=∠AEB( )
所以∠ =∠ ( )
所以AD∥BC ( )
-
科目: 来源: 题型:
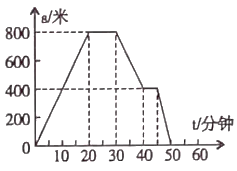
查看答案和解析>>【题目】在周末,小花晚饭后外出散步遇见同学,交谈了一会儿,然后返回,返回途中在报亭看了一会报纸才回到家,如图是根据此情景画出的图象,请回答下列问题:
(1)小花是在距家 米处遇见同学的,交谈了 分钟时间.
(2)报亭离家 米远.
(3)小花在整个过程中走得最快时的速度是 米/分钟.
-
科目: 来源: 题型:
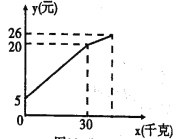
查看答案和解析>>【题目】一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)降价前他每千克萝卜出售的价格是多少?
(2)降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
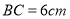 ,将△ABC以每秒2cm的速度沿
,将△ABC以每秒2cm的速度沿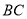 所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使
所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使 成立,则
成立,则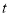 的值为_____秒.
的值为_____秒.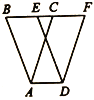
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

相关试题

