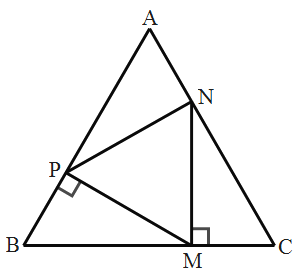
【题目】如图,点P、M、N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PV⊥AC于点N,若AB=12cm,求CM的长为______cm.
参考答案:
【答案】4
【解析】
根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,根据平角的义即可得出∠NPM=∠PMN=∠MNP,即可证△PMN是等边三角形:根据全等三角形的性质得到PA=BM=CN,PB=MC=AN,从而求得MC+NC=AC=12cm,再根据直角三角形30°角所对的直角边等于斜边的一半得出2MC=NC,即司得MC的长.
∵△ABC是等边三角形,∴∠A=∠B=∠C.
∵MP⊥AB,MN⊥BC,PN⊥AC,∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形∴PN=PM=MN,∴△PBM≌△MCN≌△NAP(AAS),
∴PA=BM=CN,PB=MC=AN,MC+NC=AC=12cm,
∵∠C=60°,∴∠MNC=30°,
∴NC=2CM,∴MC+NC=3CM=12cm,∴CM=4cm.
故答案为:4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意抛掷一枚均匀的骰子,朝上面的点数为
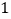 的概率为
的概率为 ,下列说法正确吗?为什么?
,下列说法正确吗?为什么?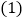 任意抛掷一枚均匀的骰子
任意抛掷一枚均匀的骰子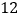 次,朝上面的点数为
次,朝上面的点数为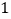 的次数为
的次数为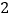 次.
次.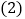 任意抛掷一枚均匀的骰子
任意抛掷一枚均匀的骰子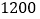 次,朝上面的点数为
次,朝上面的点数为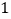 的次数大约为
的次数大约为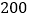 次.
次. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( )
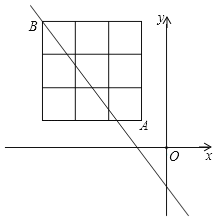
A.
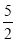 B.
B.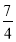 C.2D.
C.2D.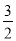
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个纸盒内有
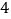 张完全相同的卡片,分别标号为
张完全相同的卡片,分别标号为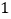 ,
,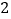 ,
,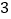 ,
,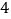 .随机抽取一张卡片后不放回,再随机抽取另一张卡片.
.随机抽取一张卡片后不放回,再随机抽取另一张卡片.(1)用列举法求“两次抽出卡片的标号等于
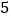 ”的概率;
”的概率;(2)小明同学连续做了
 次试验,这
次试验,这 次试验没有一次出现“两次抽出卡片的标号和等于
次试验没有一次出现“两次抽出卡片的标号和等于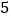 ”.他说,“第
”.他说,“第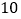 次试验我一定能够‘两次抽出卡片的标号和等于
次试验我一定能够‘两次抽出卡片的标号和等于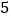 ’”.你认为他说得对吗,为什么?
’”.你认为他说得对吗,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
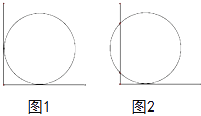
A. 25cm B. 30cm C. 50cm D. 60cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:黄瓜的种植成本是1元/kg,售价为1.5元/kg;茄子的种植成本是1.2元/kg,售价是2元/kg.
(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,BE平分∠ABC,DE∥BC.

(1)试猜想△BDE的形状,并说明理由;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
相关试题

