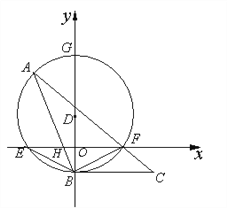
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
参考答案:
【答案】(1)直线BC与⊙D相切,理由见解析;
(2)证明见解析;
(3)F(4,0),A(-4.8,4.4)
【解析】试题分析:(1)连FG,要证BC是切线,只需证∠DBC=90°,即证∠DBF+∠CBF=90°,而∠CBF=∠A,∠A=∠BGF,又∠BGF+∠DBF=90°,则可证明.
(2)连AE,则得到母子三角形的基本图形,结合垂径定理和圆周角定理证明△BEH∽△BAE即可.
(3)求坐标,作垂线,所以过点A分别向坐标轴作垂线,结合相似三角形的性质求出AQ,OQ的长即可.
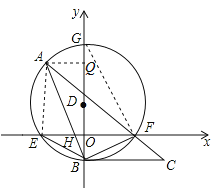
试题解析(1)直线BC与⊙D相切.
证明:如图,连接GF,∵BG是⊙D直径,∴∠GFB=90°.
∴∠G+∠GBF=90°,
∵∠A=∠G ,∠FBC=∠A,∴∠G=∠FBC,
∴∠FBC+∠GBF=90°,即∠GBC=90°,
∴直线BC与⊙D相切.
(2) 如图,连接AE.
∵BG⊥EF, BG是⊙D直径.
∴![]() ,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
∴![]() ∴BE2=BH·AB.
∴BE2=BH·AB.
(3) 作AQ⊥GB,∵E(-4,0),根据垂径定理得,OE=OF=4,∴F(4,0) .
∵BE2=BH·AB, BE2=OE2 +OB2=16+4=20, AB=8,∴BH=2.5,得OH=1.5 .
由△BOH∽△BQA,得![]() AQ=4.8,BQ=6.4.
AQ=4.8,BQ=6.4.
∴OQ=4.4 ,∴A(-4.8,4.4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x2=x4
B.x2+x3=2x5
C.3x﹣2x=1
D.x2y﹣2x2y=﹣x2y -
科目: 来源: 题型:
查看答案和解析>>【题目】某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.
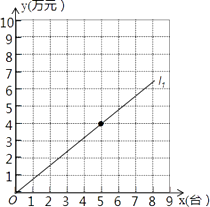
(1)直线l1对应的函数表达式是 , 每台电脑的销售价是万元;
(2)写出商场一天的总成本y2(万元)与销售量x(台)之间的函数表达式:;
(3)在图的直角坐标系中画出第(2)小题的图象(标上l2);
(4)通过计算说明:每天销售量达到多少台时,商场可以盈利. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题: ①两条直线被第三条直线所截,同位角相等;
②0.1 的算术平方根是0.01;
③算术平方根等于它本身的数是1;
④如果点P(3﹣2n,1)到两坐标轴的距离相等,则n=1;
⑤若a2=b2 , 则a=b;
⑥若 =
=  ,则a=b.
,则a=b.
其中假命题的个数是( )
A.3个
B.4 个
C.5个
D.6个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=0是关于y的一元二次方程(m﹣1)y2+my+4m2﹣4=0的一个根,那么m的值是( )
A. 0B. ±1C. 1D. ﹣1
-
科目: 来源: 题型:
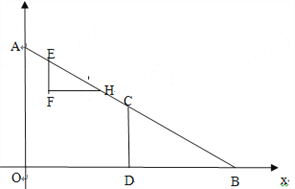
查看答案和解析>>【题目】如图,在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA,点E从点A出发,以每秒1个单位的速度向B运动,到点B停止,AE=EF,运动时间为t(s).
(1)在Rt△EFH中,EF= ,EH= ,点F坐标为( , )(用含t的代数式表示)
(2)t为何值时,H与C重合?
(3)设△EFH与△CDB重叠部分图形的面积为S(S>0),求S与t的函数关系式。
(4)在整个运动过程中,Rt△EFH扫过的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过A(-2, 0), C(0, 6)两点的抛物线y=-
 x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.
x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.(1)求a、b的值;
(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.随着点P的运动,若以A、P、Q、C为顶点的四边形是平行四边形,请直接写出符合条件的点Q的坐标;
(3)在直线AC上是否存在一点M,使△BDM的周长最小,若存在,请找出点M并求出点M的坐标.若不存在,请说明理由。


备用图
相关试题

