【题目】2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:
平日票价(元/张) | 指定日票价(元/张) | 三次票(元/张) | |
普通票 | 120 | 160 | 300 |
优惠票 | 80 | 100 |
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?
(2)如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?
参考答案:
【答案】(1)普通票6张,优惠票4张;(2)最多可以买5张三次票,两种购票方案
【解析】
(1)设需购买普通票x张,优惠票y张,根据小明,小亮两家共10人,购买门票共用去1360元列方程组求解即可;
(2)法1根据题意列出不等式求解;法2根据不考虑三次票的话及全买三次票求出三次票的范围,再讨论即可.
解:(1)设需购买普通票x张,优惠票y张,
依题有![]() ,
,
得![]() ,
,
答:他们需购买普通票6张,优惠票4张;
(2)法1:设他们买了x张三次票,则3<x<7,x为整数,
他们平日去参观世园会,如果不考虑三次票的话,
∵买票需![]() 元,
元,
∴剩下![]() 元,
元,
![]() ,
,
![]() ,
,
![]() ,
,
依题有 ![]() ,
,
得![]() ,
,
又 ![]() x为整数,
x为整数,
![]()
![]() ,
,
答:此时最多可以买5张三次票.
法2:他们平日去参观世园会,如果不考虑三次票的话,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故可以买4张,5张或6张三次票,
讨论:i)若买4张三次票,则![]() ,
,
∴可保证游玩.
ii)若买5张三次票,则
![]() ,
,![]() ,
,
又∵500>440,
∴可保证游玩.
iii)若买6张三次票,则![]() ,
,
∴不可保证游玩.
答:他们最多可以买5张三次票,买5张三次票的前提下共有以下两种购票方案,分别为:三次票5张,普通票1张,优惠票4张;三次票5张,普通票2张,优惠票3张;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅计划购买12张餐桌和一批椅子(不少于12把),现从甲、乙两商场了解到同一型号的餐桌报价都为每张200元,餐椅报价都为每把50元.甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八五折销售,那么,什么情况下到甲商场购买更优惠.
-
科目: 来源: 题型:
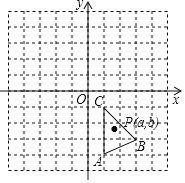
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
(1)将△ABC先向上平移5个单位,再向左平移3个单位,画出平移后得到的△A1B1C1;
(2)写出△A1B1C1各顶点的坐标;
(3)若△ABC内有一点P(a,b),请写出平移后得到的对应点P1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.

-
科目: 来源: 题型:
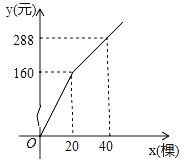
查看答案和解析>>【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
-
科目: 来源: 题型:
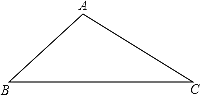
查看答案和解析>>【题目】下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到
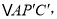 连接
连接 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明: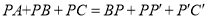 ;
;问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.

相关试题

