【题目】 如图,在长方形![]() 中,
中,![]() ,
,![]() .、点
.、点![]() 在边
在边![]() 上,将△
上,将△![]() 沿着
沿着![]() 折叠,使点
折叠,使点![]() 恰好落在对角线
恰好落在对角线![]() 上点
上点![]() 处,则
处,则![]() 的长是___________.
的长是___________.

参考答案:
【答案】5
【解析】由ABCD为矩形,得到∠BAD为直角,且三角形BEF与三角形BAE全等,利用全等三角形对应角、对应边相等得到EF⊥BD,AE=EF,AB=BF,利用勾股定理求出BD的长,由BD-BF求出DF的长,在Rt△EDF中,设EF=x,表示出ED,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出DE的长.
解:∵矩形ABCD,
∴∠BAD=90°,
由折叠可得△BEF≌△BAE,
∴EF⊥BD,AE=EF,AB=BF,
在Rt△ABD中,AB=CD=6,BC=AD=8,
根据勾股定理得:BD=10,即FD=106=4,
设EF=AE=x,则有ED=8x,
根据勾股定理得:x2+42=(8x)2,
解得:x=±3(负值舍去),
∴DE=83=5.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】广州市体育中考项目改为耐力跑后,某体育用品商场预测某款运动鞋能够畅销,就用16000元购进了一批这款运动鞋,上市后很快脱销,商场又用40000元购进第二批这款运动鞋,所购数量是第一批的2倍,但每双鞋的进价高了10元.求该款运动鞋第一次进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=5是方程ax﹣8=20+a的解,则a的值是( )
A.2
B.3
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】“赵爽炫图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽炫图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为
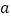 ,较短直角边长为
,较短直角边长为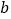 ,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
,若(a+b)2=21,大正方形的面积为13,则小正方形的边长为( )
A.
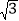 B. 2 C.
B. 2 C.  D.
D. 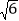
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为4和6,则第三边可能是( )
A. 2 B. 7 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的三个内角的度数分别为40°,60°,80°,则这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)
分)(
 )【问题】如图
)【问题】如图 ,点
,点 为线段
为线段 外一动点,且
外一动点,且 ,
,  .当点
.当点 位于__________时线段
位于__________时线段 的长取得最大值,且最大值为__________(用含
的长取得最大值,且最大值为__________(用含 、
、 的式子表示).
的式子表示).(
 )【应用】点
)【应用】点 为线段
为线段 除外一动点,且
除外一动点,且 ,
,  .如图
.如图 所示,分别以
所示,分别以 、
、 为边,
为边,作等边三角形
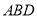 和等边三角形
和等边三角形 ,连接
,连接 、
、 .
.①请找出图中与
 相等的线段,并说明理由.
相等的线段,并说明理由.②直接写出线段
 长的最大值.
长的最大值.(
 )【拓展】如图
)【拓展】如图 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,点
,点 为线段
为线段 外一动点,且
外一动点,且 ,
,  ,
,  .请直接写出线段
.请直接写出线段 长的最大值及此时点
长的最大值及此时点 的坐标.
的坐标.



相关试题

