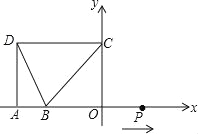
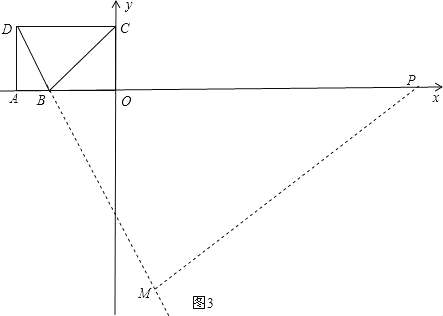
【题目】如图,在坐标系xOy中,已知D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.
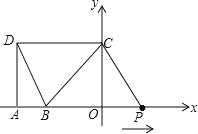
(1)当t为何值时,PC∥DB;
(2)当t为何值时,PC⊥BC;
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边(或边所在的直线)相切时,求t的值.
参考答案:
【答案】(1)2(2)![]() (3)4,12,t=(6
(3)4,12,t=(6![]() +12)
+12)
【解析】
试题分析:(1)过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,求出DC=5,OC=4,OB=3,根据四边形DBPC是平行四边形求出DC=BP=5,求出OP=2即可;
(2)证△PCO∽△CBO,得出![]() ,求出OP=
,求出OP=![]() 即可;
即可;
(3)设⊙P的半径是R,分为三种情况:①当⊙P与直线DC相切时,过P作PM⊥DC交DC延长线于M,求出PM、OP的长即可;
②当⊙P与BC相切时,根据△COB∽△PBM得出![]() ,求出R=12即可;③当⊙P与DB相切时,证△ADB∽△MPB得出
,求出R=12即可;③当⊙P与DB相切时,证△ADB∽△MPB得出![]() ,求出R即可.
,求出R即可.
试题解析:(1)∵D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,
∴DC=5,OC=4,OB=3,
∵DC⊥y轴,x轴⊥y轴,
∴DC∥BP,
∵PC∥DB,
∴四边形DBPC是平行四边形,
∴DC=BP=5,
∴OP=5﹣3=2,
2÷1=2,
即当t为2秒时,PC∥BD;
(2)∵PC⊥BC,x轴⊥y轴,
∴∠COP=∠COB=∠BCP=90∴,
∴∠PCO+∠BCO=90°,∠CPO+∠PCO=90°,
∴∠CPO=∠BCO,
∴△PCO∽△CBO,
∴![]() ,
,
∴![]() ,
,
∴OP=![]() ,
,
![]() ÷1=
÷1=![]() ,
,
即当t为![]() 秒时,PC⊥BC;
秒时,PC⊥BC;
(3)设⊙P的半径是R,
分为三种情况:①当⊙P与直线DC相切时,
如图1,过P作PM⊥DC交DC延长线于M,
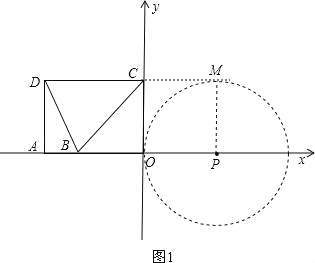
则PM=OC=4=OP,
4÷1=4,
即t=4;
②如图2,当⊙P与BC相切时,
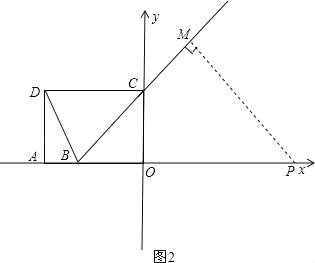
∵∠BOC=90°,BO=3,OC=4,由勾股定理得:BC=5,
∵∠PMB=∠COB=90°,∠CBO=∠PBM,
∴△COB∽△PMB,
∴![]() ,
,
∴![]() ,
,
R=12,
12÷1=12,
即t=12秒;
③根据勾股定理得:BD=![]() =2
=2![]() ,
,
如图3,当⊙P与DB相切时,
∵∠PMB=∠DAB=90°,∠ABD=∠PBM,
∴△ADB∽△MPB,
∴![]() ,
,
∴![]() ,
,
R=6![]() +12;
+12;
(6![]() +12)÷1=6
+12)÷1=6![]() +12,
+12,
即t=(6![]() +12)秒.
+12)秒.
-
科目: 来源: 题型:
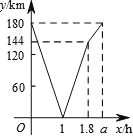
查看答案和解析>>【题目】甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.
(1)求甲车行驶的速度.
(2)求甲车到达B地后y与x之间的函数关系式.
(3)当两车相遇后,两车之间的路程是160km时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“五一”劳动节,某中学组织了甲、乙两个义务劳动小组,甲组x人,乙组y人,到“中华路”和“青年路”打扫卫生,根据打扫卫生的进度,学校随时调整两组人数,如果从甲组调50人去乙组,则乙组人数为甲组人数的2倍;如果从乙组调m人去甲组,则甲组人数为乙组人数的3倍.
(1)求出x与m之间的函数表达式.
(2)问:当m为何值时,甲组人数最少,最少是多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=
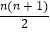 .
.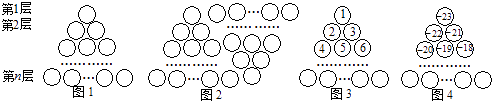
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
﹣23,﹣22,﹣21,﹣20,…,则所有圆圈中各数之和为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】汽车以每小时60千米的速度匀速行驶,行驶路程为s千米,行驶的时间为t小时,则s与t的函数解析式为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如表:
收费标准(注:水费按月结算)
每月用水量
单价:元/立方米
不超出8立方米(含8立方米)部分
2.8
超出8立方米,不超出12立方米(含12立方米)部分
3.6
超出12立方米部分
4.8
请根据上表的内容解答下列问题:
(1)若某户居民11月份用水a立方米(其中8<a<12),请用含a的代数式表示应收水费.
(2)若某户居民12月份交水费56元,则用水量为多少立方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是一元二次方程x2﹣x﹣1=0的两根,则2x12﹣x1+x22=_____.
相关试题

