【题目】关于x的方程x2﹣(2k﹣1)x+k2﹣2k+3=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为x1、x2 , 存不存在这样的实数k,使得|x1|﹣|x2|= ![]() ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
参考答案:
【答案】
(1)解:∵方程有两个不相等的实数根,
∴△=[﹣(2k﹣1)]2﹣4(k2﹣2k+3)=4k﹣11>0,
解得:k> ![]() ;
;
(2)解:存在,
∵x1+x2=2k﹣1,x1x2=k2﹣2k+3=(k﹣1)2+2>0,
∴将|x1|﹣|x2|= ![]() 两边平方可得x12﹣2x1x2+x22=5,即(x1+x2)2﹣4x1x2=5,
两边平方可得x12﹣2x1x2+x22=5,即(x1+x2)2﹣4x1x2=5,
代入得:(2k﹣1)2﹣4(k2﹣2k+3)=5,
解得:4k﹣11=5,
解得:k=4.
【解析】(1)一元二次方程有两个不相等的实数根的条件是判别式![]() >0,构建关于k的不等式,解出不等式即可;(2)先由两根之积x1x2=k2﹣2k+3=(k﹣1)2+2>0,判断出二者同号, 可去绝对值:同正,|x1|﹣|x2|=x1-x2,同负,|x1|﹣|x2|=-(x1-x2),然后两边同时平方,即可求出k.
>0,构建关于k的不等式,解出不等式即可;(2)先由两根之积x1x2=k2﹣2k+3=(k﹣1)2+2>0,判断出二者同号, 可去绝对值:同正,|x1|﹣|x2|=x1-x2,同负,|x1|﹣|x2|=-(x1-x2),然后两边同时平方,即可求出k.
【考点精析】关于本题考查的求根公式和根与系数的关系,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
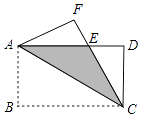
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:
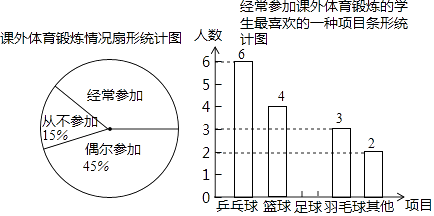
根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一列数-1,2,-1,2,2,-1,2,2,2,-1,…其中相邻的两个-1被2隔开,第n对-1之问有n个2,则第21个数是______,这一列数的前2019个数的和为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:

 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______. 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______. 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
相关试题

