【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.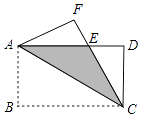
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°,
∵将矩形ABCD沿对角线AC翻折,点B落在点F处,
∴∠F=∠B,AB=AF,
∴AF=CD,∠F=∠D,
在△AEF与△CDE中, 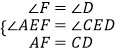 ,
,
∴△AFE≌△CDE;
(2)解:∵AB=4,BC=8,
∴CF=AD=8,AF=CD=AB=4,
∵△AFE≌△CDE,
∴AE=CE,EF=DE,
∴DE2+CD2=CE2,
即DE2+42=(8﹣DE)2,
∴DE=3,
∴EF=3,
∴图中阴影部分的面积=S△ACF﹣S△AEF= ![]() ×4×8﹣
×4×8﹣ ![]() ×4×3=10.
×4×3=10.
【解析】(1)由翻折性质可得∠F=∠B,AB=AF,再由矩形性质可得对边相等,可利用“角角边”证得全等;(2)阴影面积可转化为S△ACF﹣S△AEF,由 △AFE≌△CDE可知,面积可转化为求△CDE面积,须以DE为未知数由勾股定理建立方程,求出DE,进而求面积.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x﹣1+
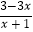 )÷
)÷ 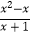 ,其中x的值从不等式组
,其中x的值从不等式组  的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=
 或
或 .其中正确的是________(填序号).
.其中正确的是________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:
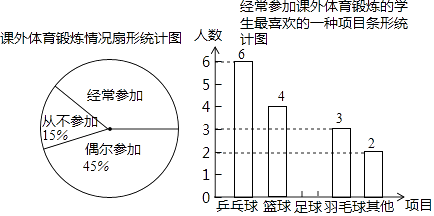
根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一列数-1,2,-1,2,2,-1,2,2,2,-1,…其中相邻的两个-1被2隔开,第n对-1之问有n个2,则第21个数是______,这一列数的前2019个数的和为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣(2k﹣1)x+k2﹣2k+3=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为x1、x2 , 存不存在这样的实数k,使得|x1|﹣|x2|=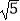 ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
相关试题

