【题目】如图,△ ABC中,AB=BC,M、N为BC边上的两点,并且∠BAM=∠CAN,MN=AN,则∠MAC= 度.
参考答案:
【答案】60
【解析】
设∠CAN=x,∠MAN=y,先表示出∠C为2x+y,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠ANM,再根据等边对等角的性质求出∠AMN=∠MAN,然后利用三角形的内角和定理列式求出x+y的度数,也就是∠MAC的度数.
解:设∠CAN=x,∠MAN=y,
∵AB=BC,∠BAM=∠CAN,
∴∠C=∠BAC=2x+y,
∴∠ANM=x+(2x+y)=3x+y,
∵MN=AN,
∴∠AMN=∠MAN,
在△AMN中,2y+(3x+y)=180°,
解得x+y=60°,
即∠MAC=60°.
故填60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于点A(2,0),B(4,0),且过点C(0,4).

(1)求出抛物线的表达式和顶点坐标;
(2)请你求出抛物线向左平移3个单位长度,再向上平移1.5个单位长度后抛物线的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=
 (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.其中正确的是( )

A.①②③B.①③④C.①②③④D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

-
科目: 来源: 题型:
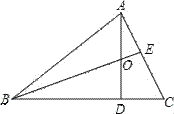
查看答案和解析>>【题目】△ABC中,AD⊥BC于点D,BE是∠ABC的平分线,已知∠ABC=40°,∠C=60°,求∠AOB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.

相关试题

