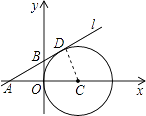
【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(2,0),直线l过点A(﹣2,0),与⊙C相切于点D,求直线l的解析式. 
参考答案:
【答案】解:如图所示,当直线l在x轴的上方时,
连接CD,
∵直线l为⊙C的切线,
∴CD⊥AD.
∵C点坐标为(2,0),
∴OC=2,即⊙C的半径为2,
∴CD=OC=2.
又∵点A的坐标为(﹣2,0),
∴AC=4,
∴AC=2CD,
∴∠CAD=30°,
在Rt△AOB中,OB=OAtan30°= ![]() ,
,
即B(0, ![]() ),
),
设直线l解析式为:y=kx+b(k≠0),则 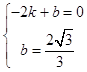 ,
,
解得k= ![]() ,b=
,b= 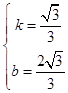 ,
,
∴直线l的函数解析式为y= ![]() x+
x+ ![]() .
.
同理可得,当直线l在x轴的下方时,直线l的函数解析式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
故直线l的函数解析式为y= ![]() x+
x+ ![]() 或y=﹣
或y=﹣ ![]() x﹣
x﹣ ![]() .
.
【解析】连接CD,由于直线l为⊙C的切线,故CD⊥AD.结合点与坐标的性质求得点B的坐标,设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
【考点精析】利用确定一次函数的表达式和切线的性质定理对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是
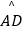 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 
(1)求∠ABC的度数;
(2)若CM=4 ,求
,求  的长度.(结果保留π)
的长度.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】王老师到坐落在东西走向的阜城大街上的文具店、书店、花店和玩具店购物,规定向东为正.已知王老师从书店购书后,走了110m到达玩具店,再走﹣75m到达花店,又继续走了﹣50m到达文具店,最后走了25m到达公交车站牌.
(1)书店距花店有多远?
(2)公交车站牌在书店的什么位置?
(3)若王老师在四个店各逗留10min,他的步行速度大约是每分钟26m,王老师从书店购书一直到公交车站一共用了多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.
(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上对七年级(1)班的8名女生做仰卧起坐测试,若以16次为达标,超过的次数用正数表示,不足的次数用负数表示.现成绩抄录如下:
+2,+2,﹣2,+3,+1,﹣1,0,+1.问:
(1)有几人达标?
(2)平均每人做几次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.

(1)求证:点E是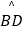 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若AD=12,⊙O的半径为10,求弦DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为
 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
相关试题

