【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G. 
(1)求证:点E是 ![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若AD=12,⊙O的半径为10,求弦DF的长.
参考答案:
【答案】
(1)证明:连接OD,如图,
∵AD∥OC,
∴∠1=∠A,∠2=∠ODA,
∵OA=OD,
∴∠A=∠ODA,
∴∠1=∠2,
∴ ![]() =
= ![]() ,即点E是
,即点E是 ![]() 的中点
的中点
(2)证明:在△OCD和△OCB中
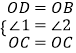 ,
,
∴△OCD≌△OCB,
∴∠ODC=∠OBC=90°,
∴OD⊥CD,
∴CD是⊙O的切线
(3)解:连接BD,
∵DF⊥AB,
∴DG=FG,
∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,BD= ![]() =
= ![]() =16,
=16,
∵ ![]() DGAB=
DGAB= ![]() ADBD,
ADBD,
∴DG= ![]() =
= ![]() ,
,
∴DF=2DG= ![]() .
.
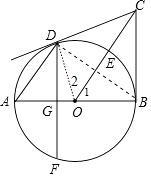
【解析】(1)连接OD,如图,根据平行线的性质得∠1=∠A,∠2=∠ODA,加上∠A=∠ODA,所以∠1=∠2,然后根据圆心角、弧、弦的关系可判断点E是 ![]() 的中点;(2)先证明△OCD≌△OCB得到∠ODC=∠OBC=90°,然后根据切线的判定方法得到结论;(3)连接BD,先根据垂径定理得到DG=FG,再利用圆周角定理得到∠ADB=90°,则可根据勾股定理计算出BD,然后利用面积法计算出DG,从而得到DF的长.
的中点;(2)先证明△OCD≌△OCB得到∠ODC=∠OBC=90°,然后根据切线的判定方法得到结论;(3)连接BD,先根据垂径定理得到DG=FG,再利用圆周角定理得到∠ADB=90°,则可根据勾股定理计算出BD,然后利用面积法计算出DG,从而得到DF的长.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.
(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(2,0),直线l过点A(﹣2,0),与⊙C相切于点D,求直线l的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上对七年级(1)班的8名女生做仰卧起坐测试,若以16次为达标,超过的次数用正数表示,不足的次数用负数表示.现成绩抄录如下:
+2,+2,﹣2,+3,+1,﹣1,0,+1.问:
(1)有几人达标?
(2)平均每人做几次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为
 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:直线AB经过点A(0,3)点B(
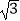 ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 
(1)求直线AB的解析式;
(2)求点M的坐标;
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次食品安检中,抽查某企业 10 袋奶粉,每袋取出 100 克,检测每 100
克奶粉蛋白质含量与规定每 100 克含量(蛋白质)比较,不足为负,超过为正, 记录如下:(注:规定每 100g 奶粉蛋白质含量为 15g)
﹣3,﹣4,﹣5,+1,+3,+2,0,﹣1.5,+1,+2.5
(1)求平均每 100 克奶粉含蛋白质为多少?
(2)每 100 克奶粉含蛋白质不少于 14 克为合格,求合格率为多少?
相关试题

